Use your data

Lecture 4

Dr. Benjamin Soltoff

Cornell University
INFO 4940/5940 - Fall 2025

September 4, 2025

Announcements

Homework 01

Learning objectives

Motivate the importance of data partitioning in machine learning
Describe common data partitioning strategies
Evaluate the potential for information leakage
Introduce resampling methods for model assessment
Demonstrate common resampling methods

Why partition data?

Data splitting and spending

For machine learning, we typically split data into training and test sets:

The training set is used to train/fit a model.
The test set is used to find an independent assessment of model performance.

Do not 🚫 use the test set during training. But why?

Meet the Palmer penguins

`penguins`

Rows: 344
Columns: 8
$ species     <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adelie…
$ island      <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgersen, Torgersen, Torgersen, T…
$ bill_len    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, 42.0, 37.8, 37.8, 41.1, 38…
$ bill_dep    <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, 20.2, 17.1, 17.3, 17.6, 21…
$ flipper_len <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186, 180, 182, 191, 198, 185,…
$ body_mass   <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, 4250, 3300, 3700, 3200, 38…
$ sex         <fct> male, female, female, NA, female, male, female, male, NA, NA, NA, NA, female, …
$ year        <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, …

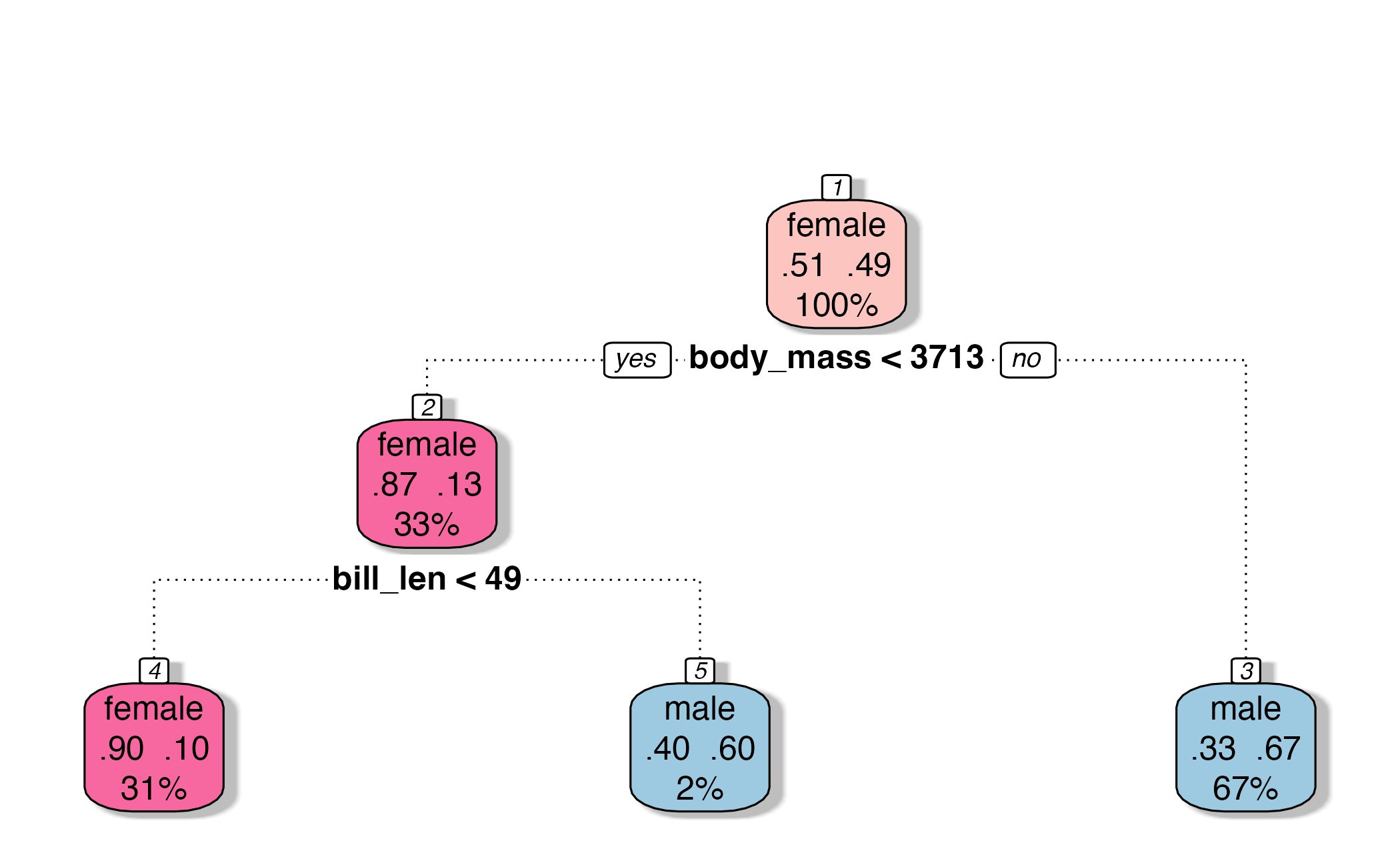
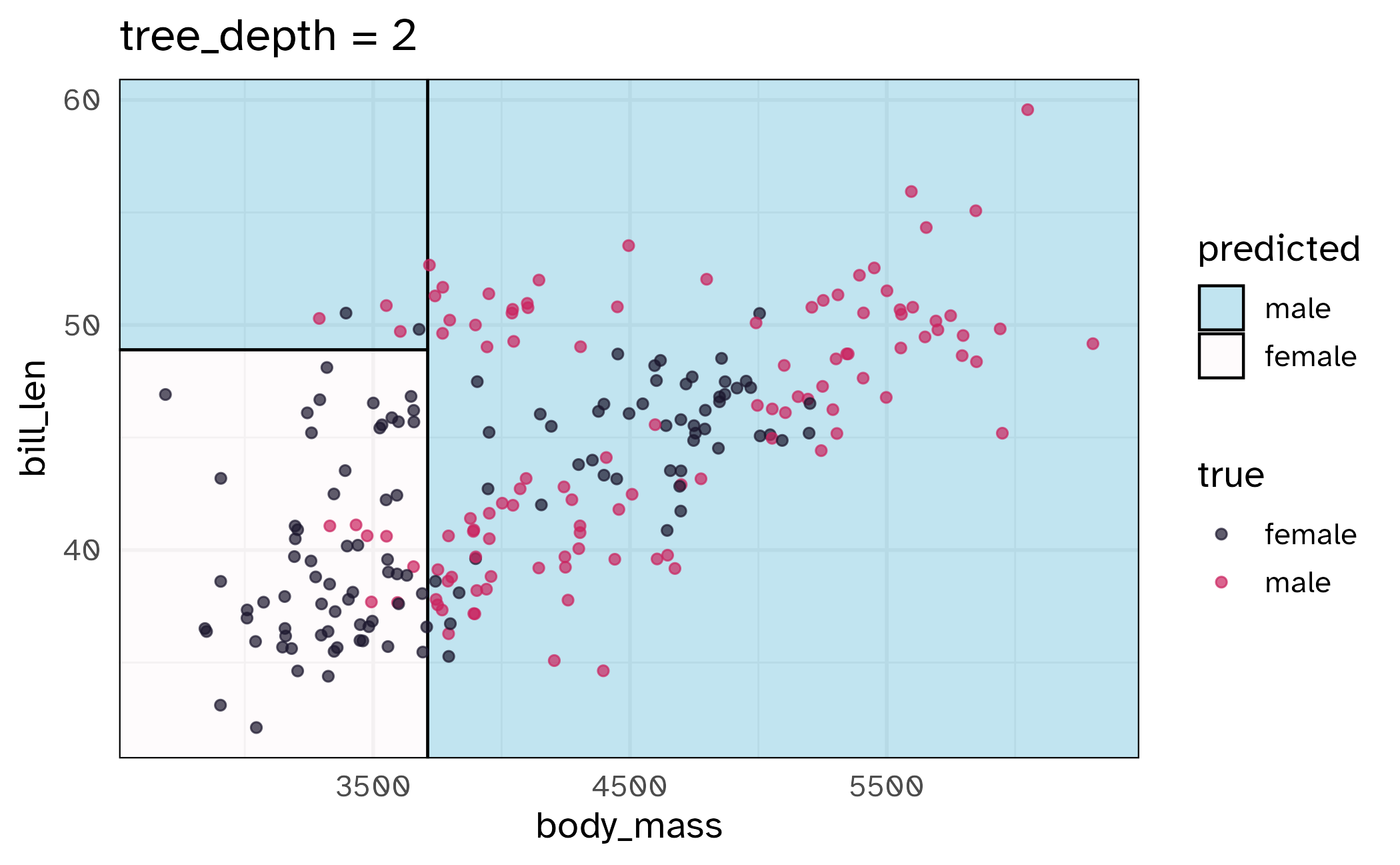
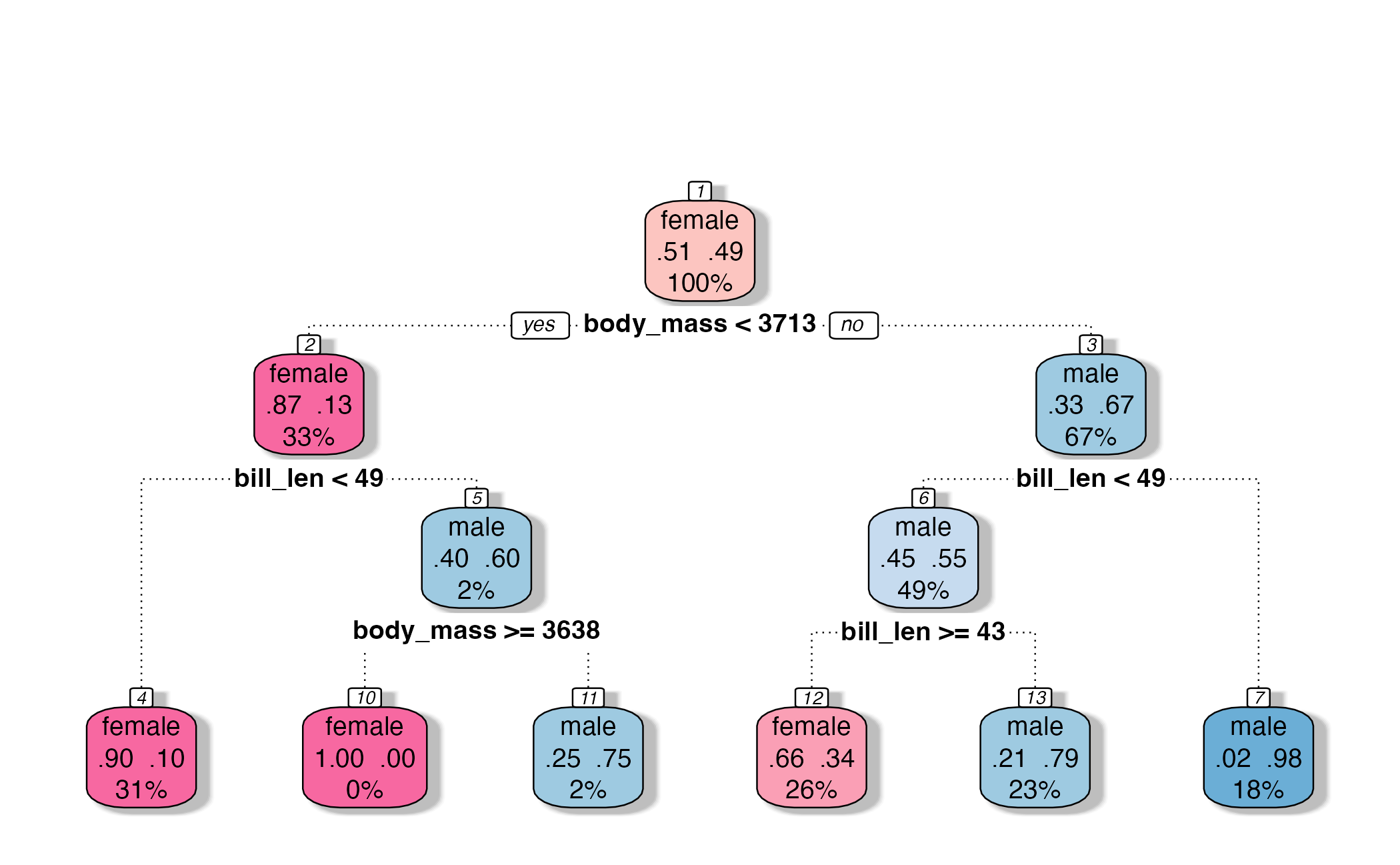
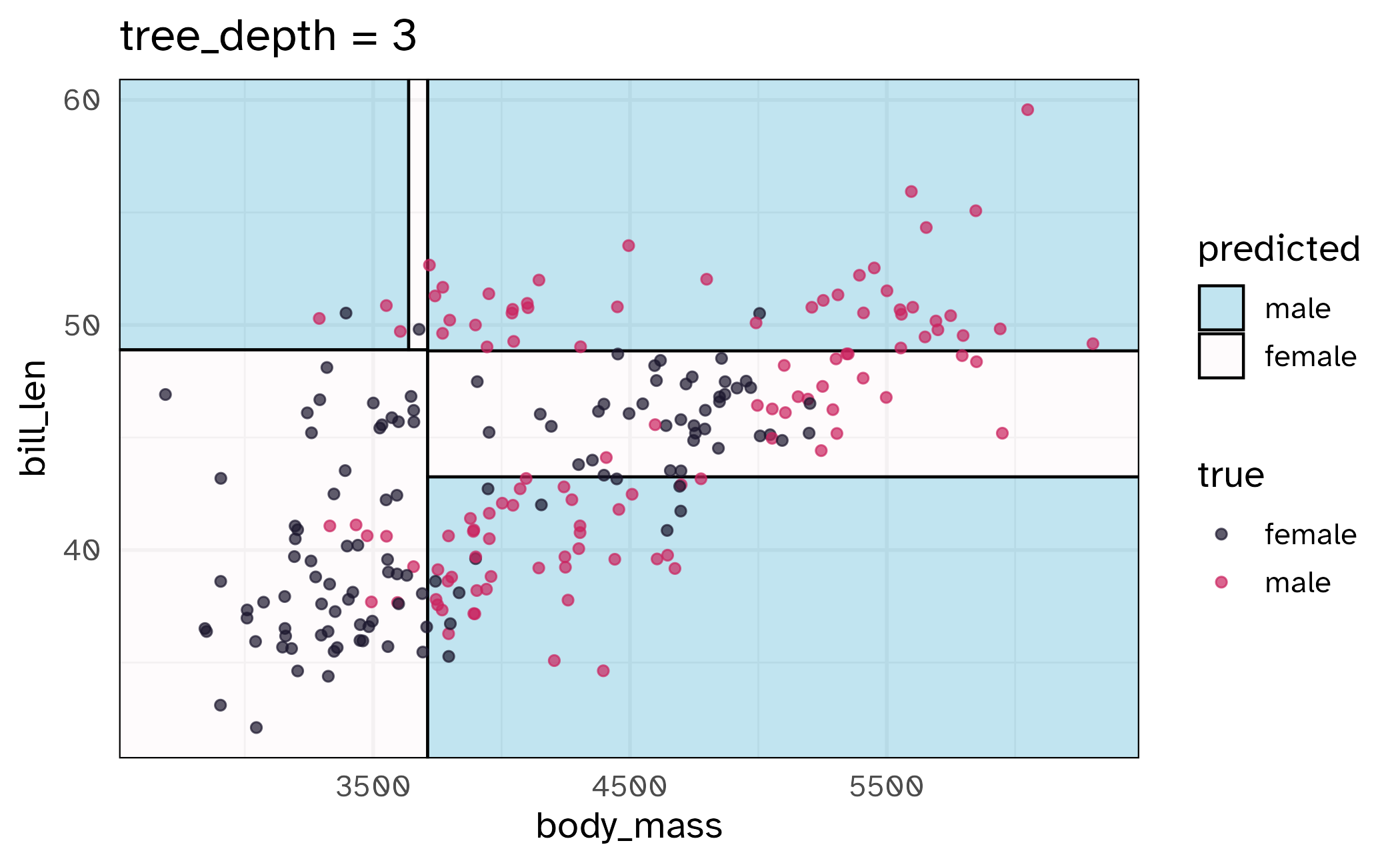
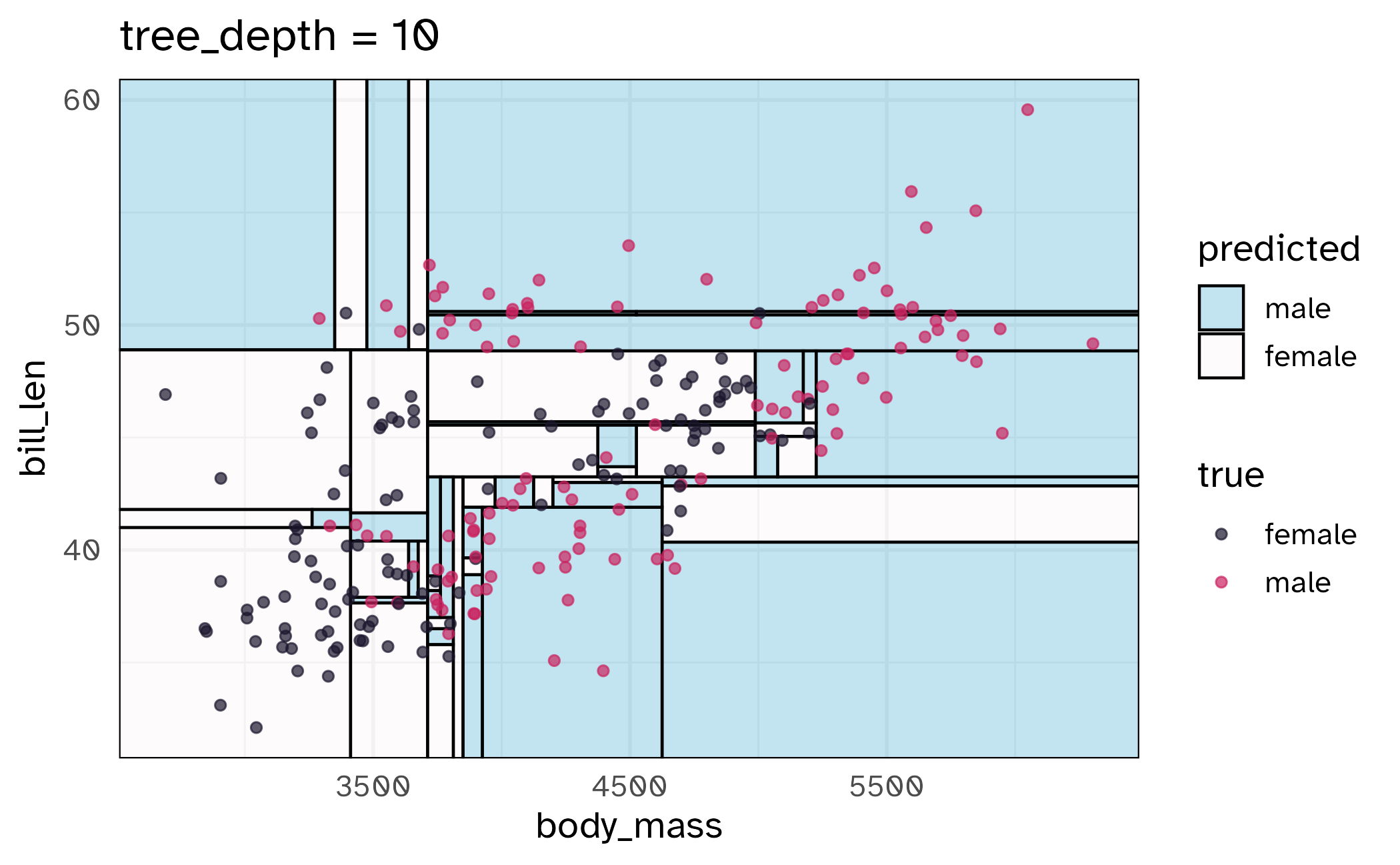
How might we spend our data?

Training a model
Comparing multiple models
Tuning hyperparameters
Estimating model performance
Selecting relevant features
Exploring the data

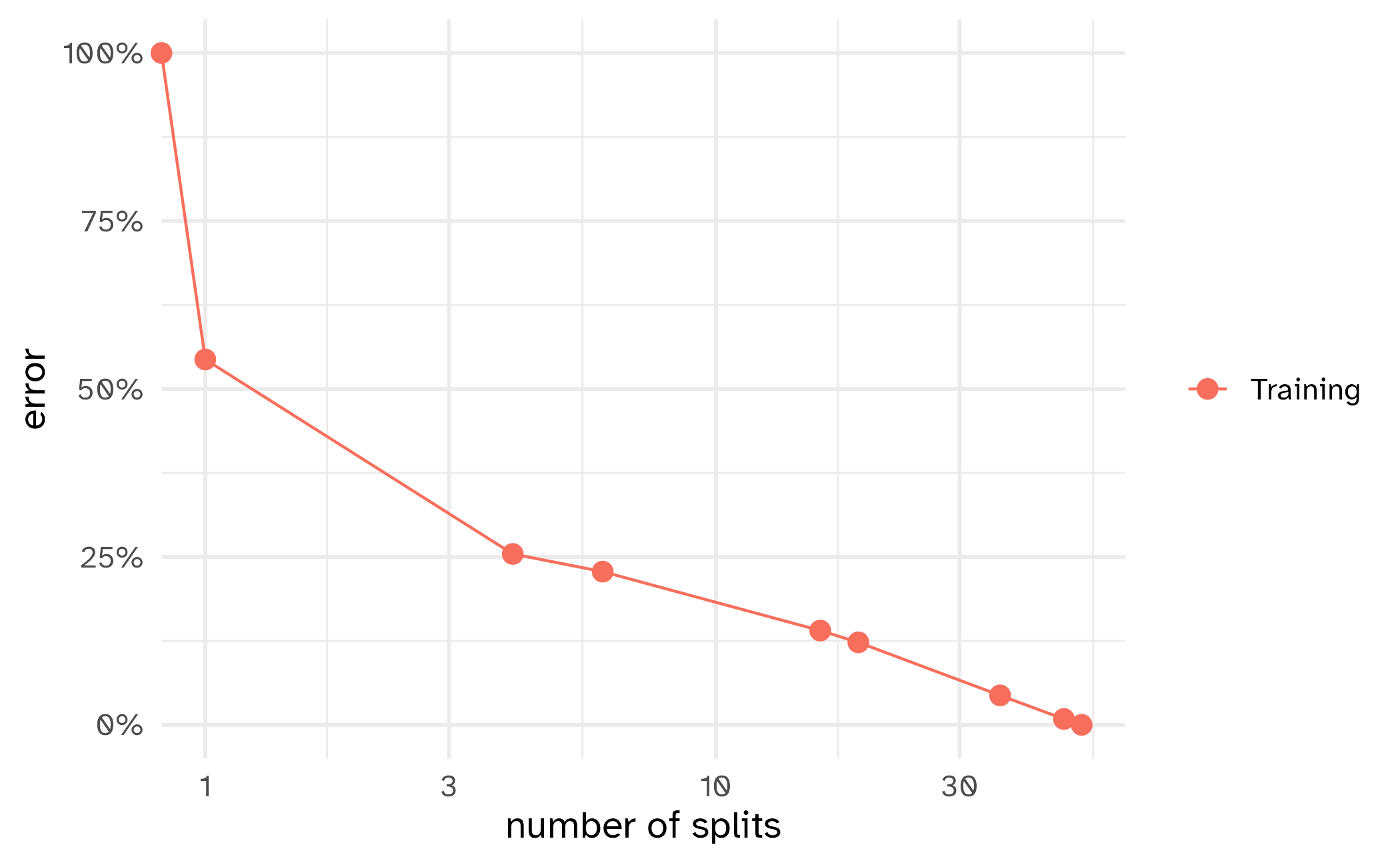
Typically our data is finite and limited, so we have to be careful how we spend it.

Simple data partitioning

The holdout method

Training set: model building and testing
Test set: final model assessment

How do we split?

Goal is to ensure no meaningful differences between sets
Randomization process to assign observations to sets
How much do we allocate to training vs. testing?
- Depends on the size of the dataset
- Enough observations in training set to learn patterns, but also enough in test set to get a reliable estimate of performance

Simple random sampling

📝 Is simple random sampling appropriate?

Instructions

For each predictive problem, decide whether simple random sampling is appropriate or not. If not, suggest an alternative.

Medical AI for emergency diagnosis
- Dataset: 50,000 emergency room visits from 3 hospitals (Hospital A: 35,000 cases, Hospital B: 10,000 cases, Hospital C: 5,000 cases)
- Goal: Predict whether patients need immediate surgery based on symptoms and vital signs
Climate change prediction model
- Dataset: Daily temperature and weather measurements from 1980-2023 across 200 weather stations
- Goal: Predict future temperature trends for the next 5 years

07:00

Information leakage

Model uses information that would not be available at prediction time

Train-test contamination: information from the test set leaks into the training process

Data preprocessing
Feature selection
Time dependency

📝 Preventing information leakage

Instructions

You’re building a model to predict house prices. Your workflow includes:

Calculating neighborhood average prices as a feature
Removing outliers (houses > $2M)
Normalizing all price-related features
Training a regression model

At what point should you split your data? Identify potential sources of information leakage and explain how your timing prevents them.

03:00

Using the training set

We should not use the test set until the very end of the analysis.

We also should not use the same observations to both train and evaluate the model.

So how do we use the training set to estimate a model and evaluate its performance without biasing our results?

Resampling methods

Data Splitting

Resampling methods

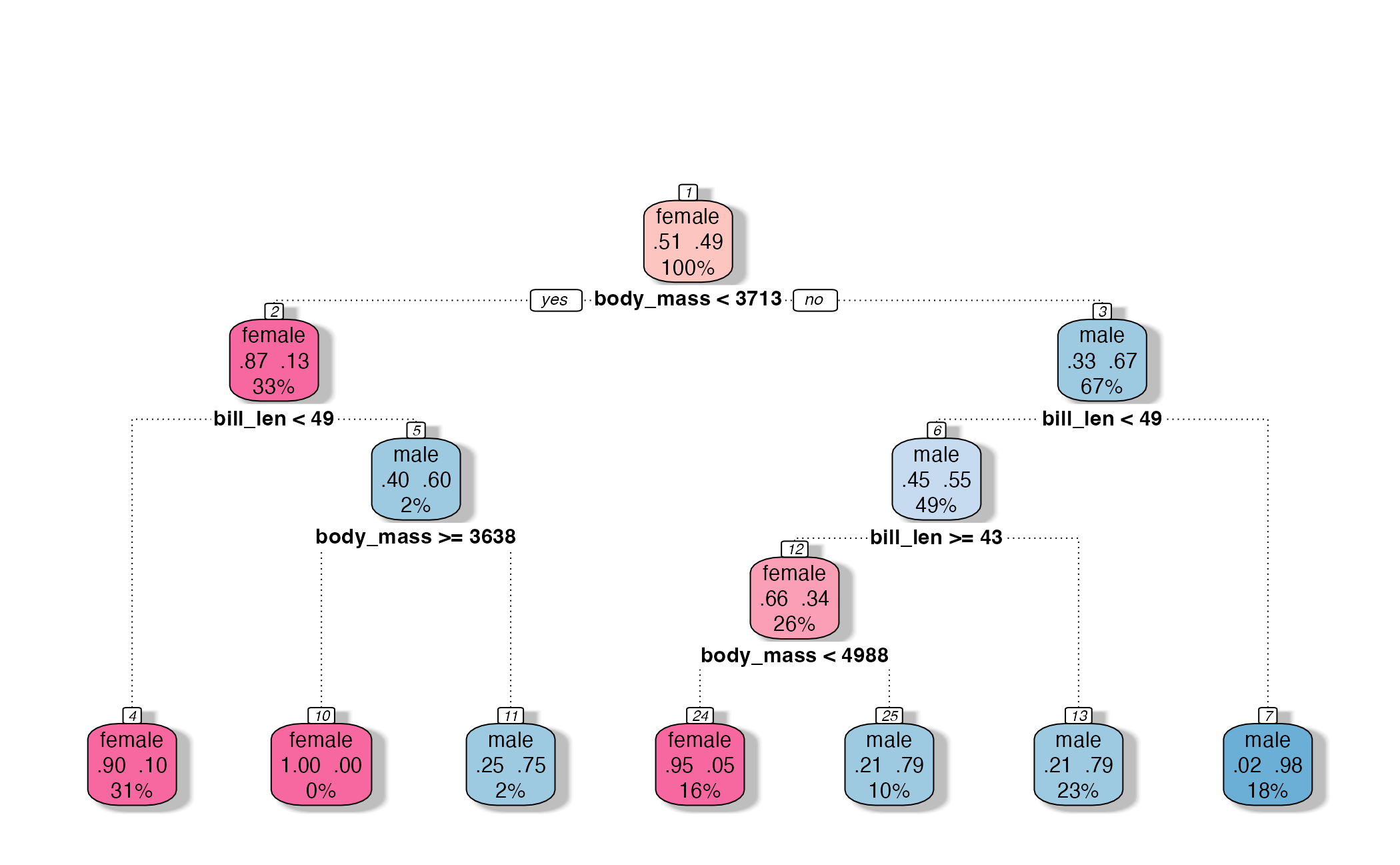
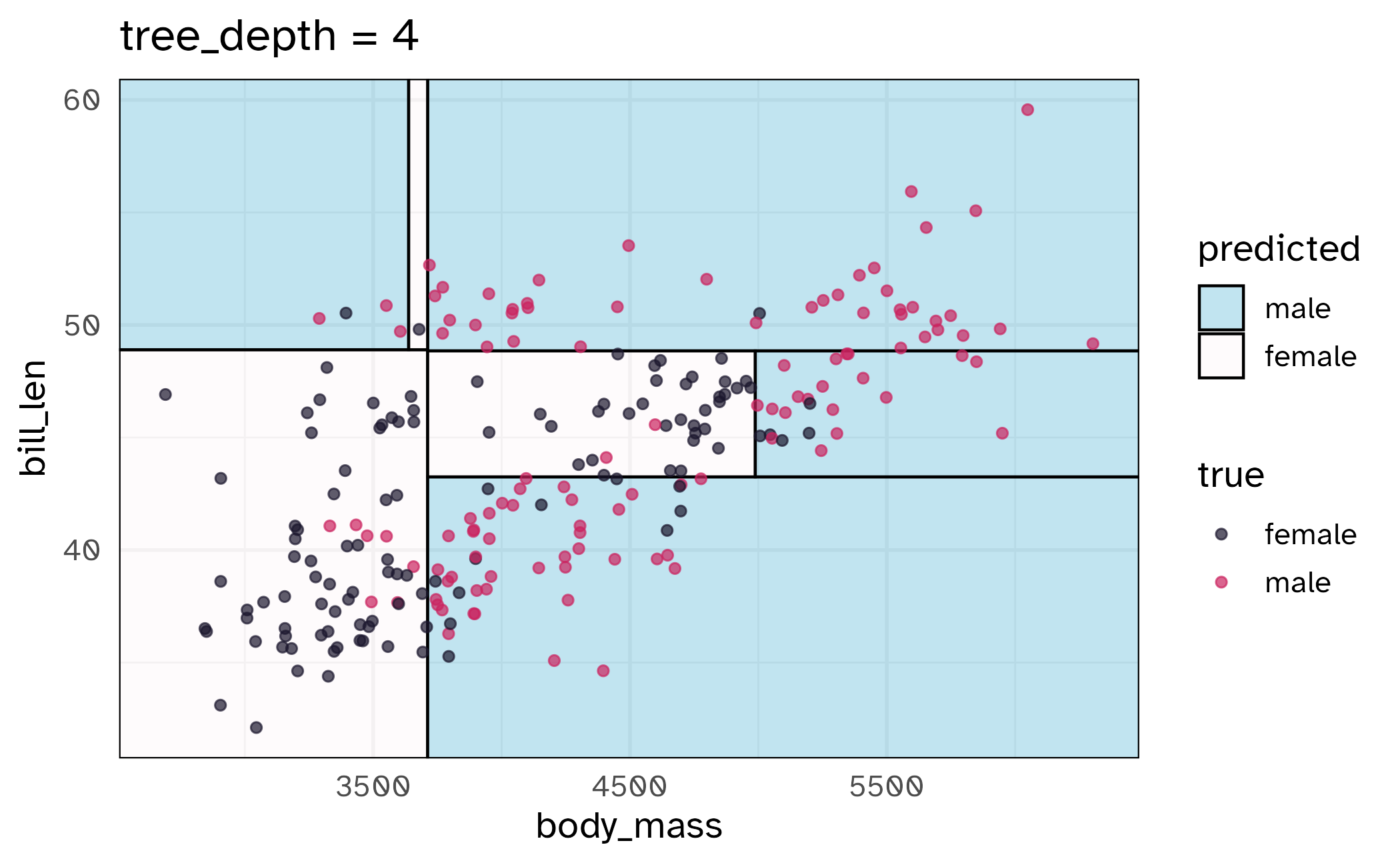
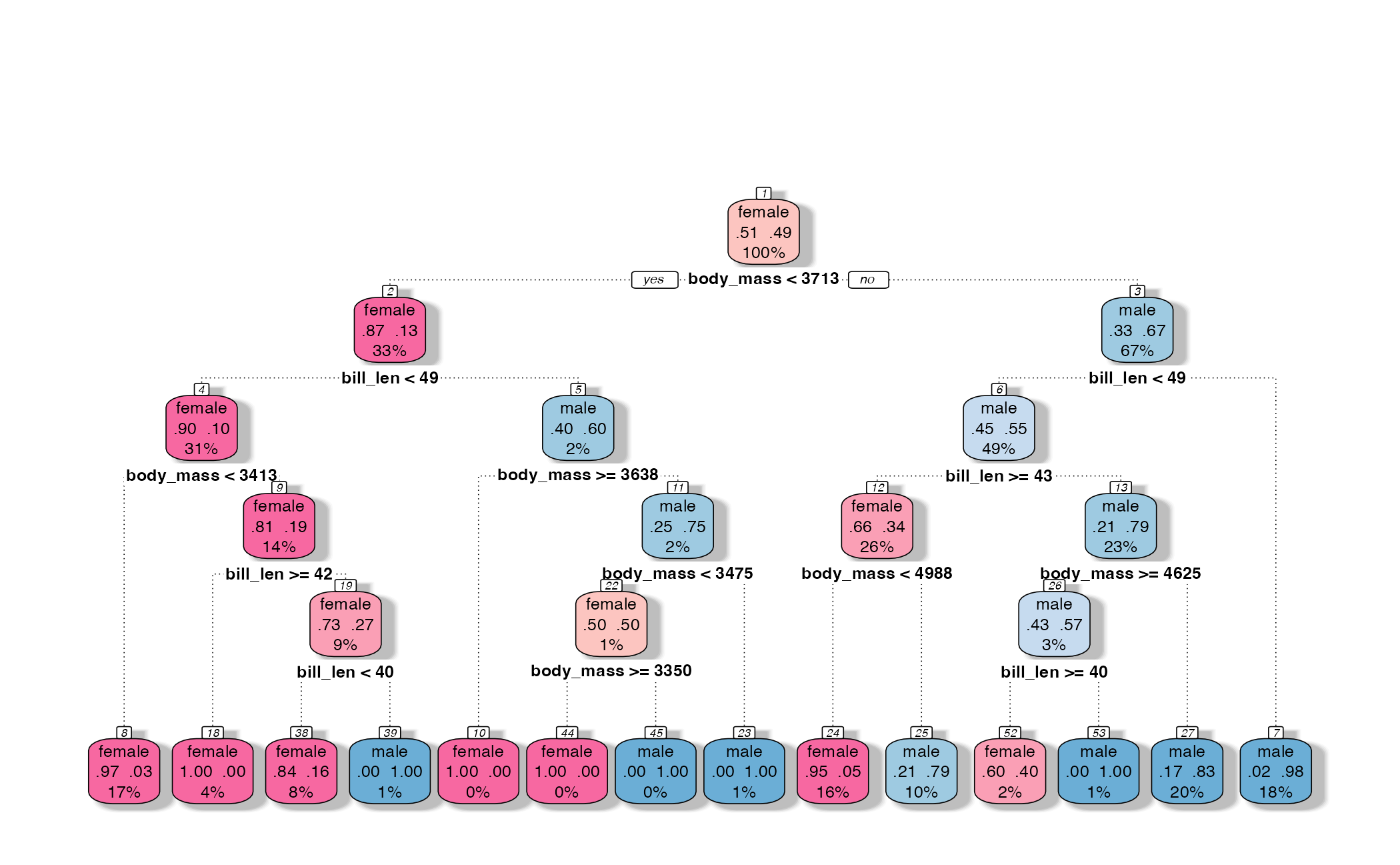
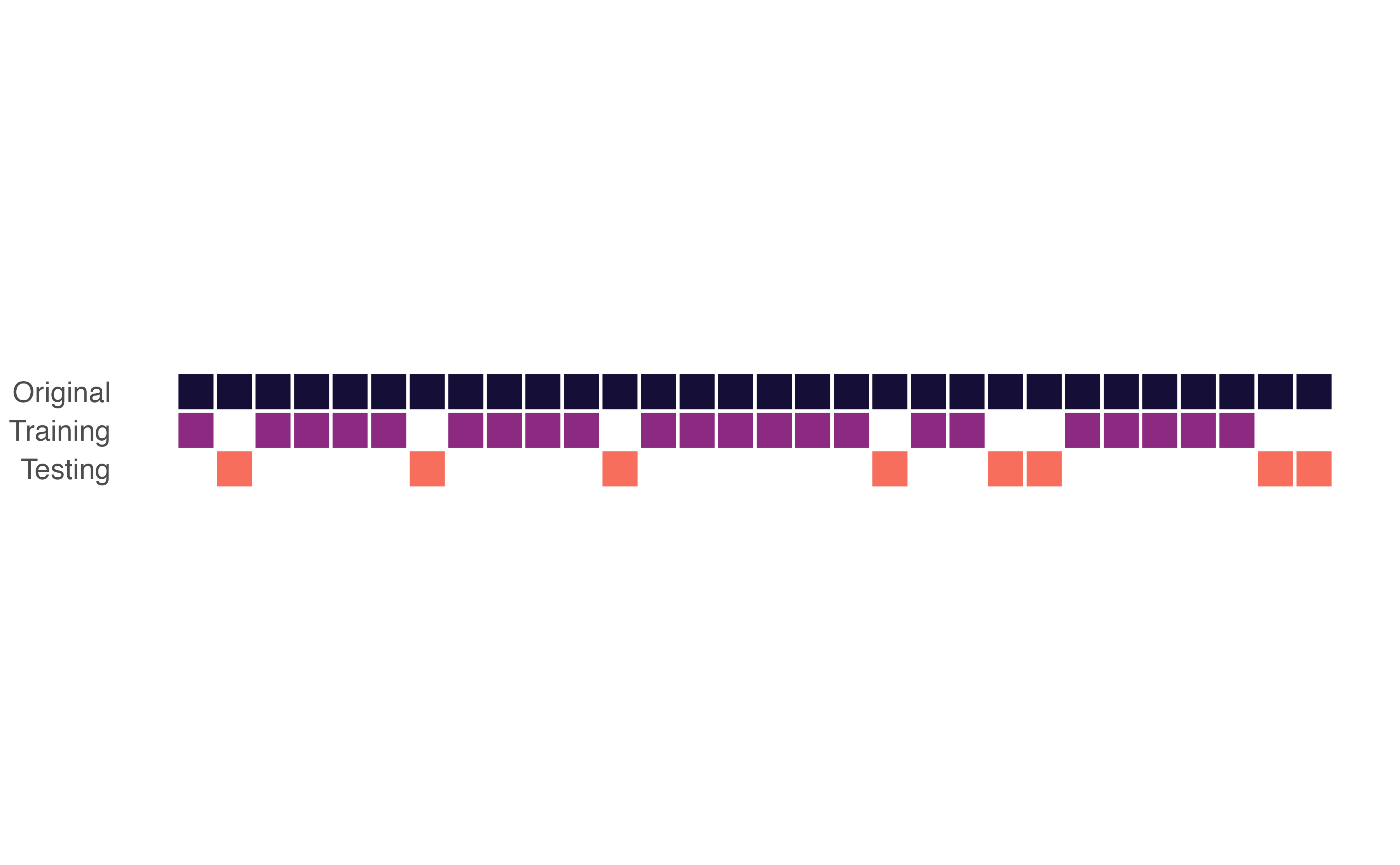
$V$-fold cross-validation

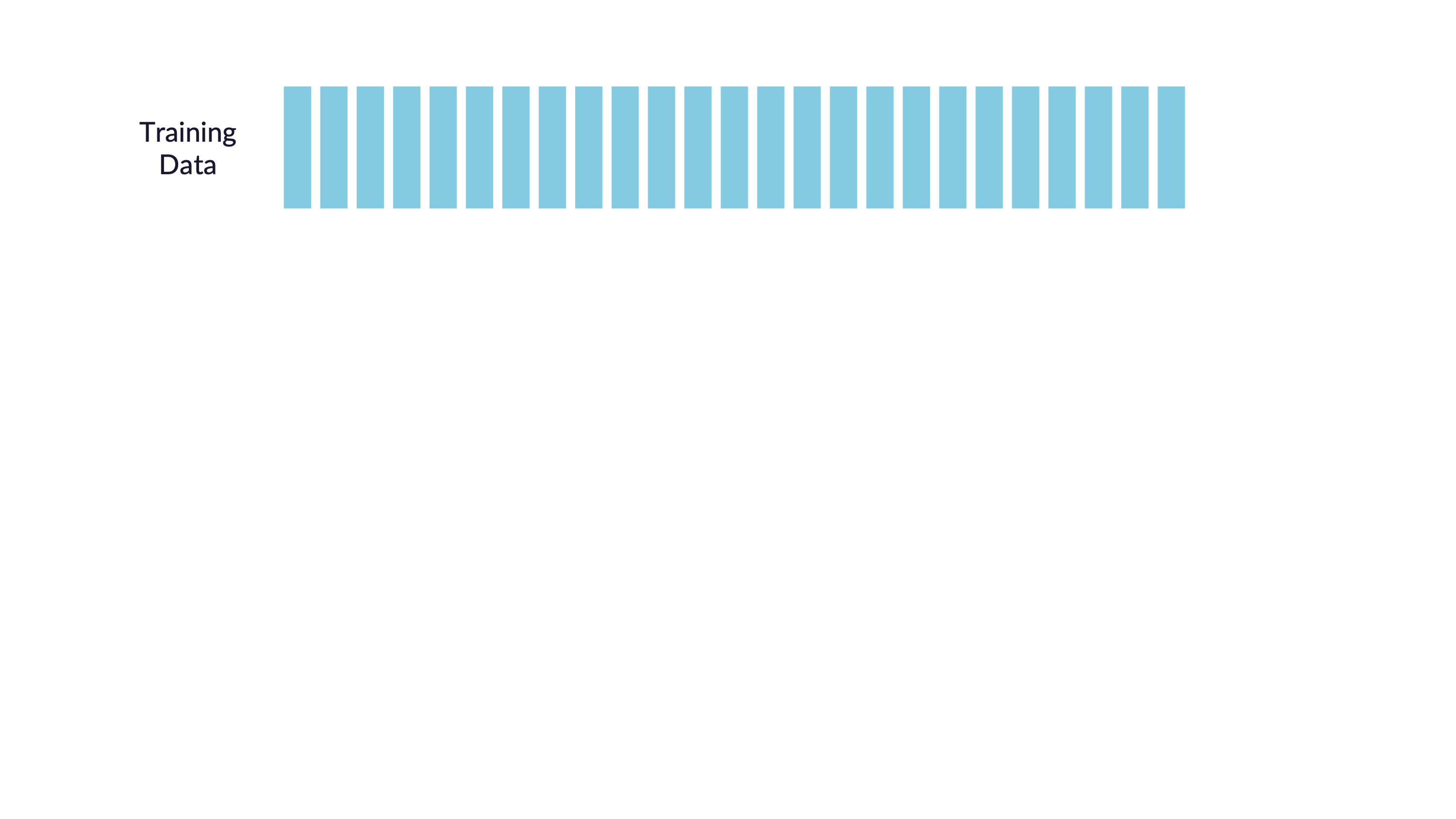
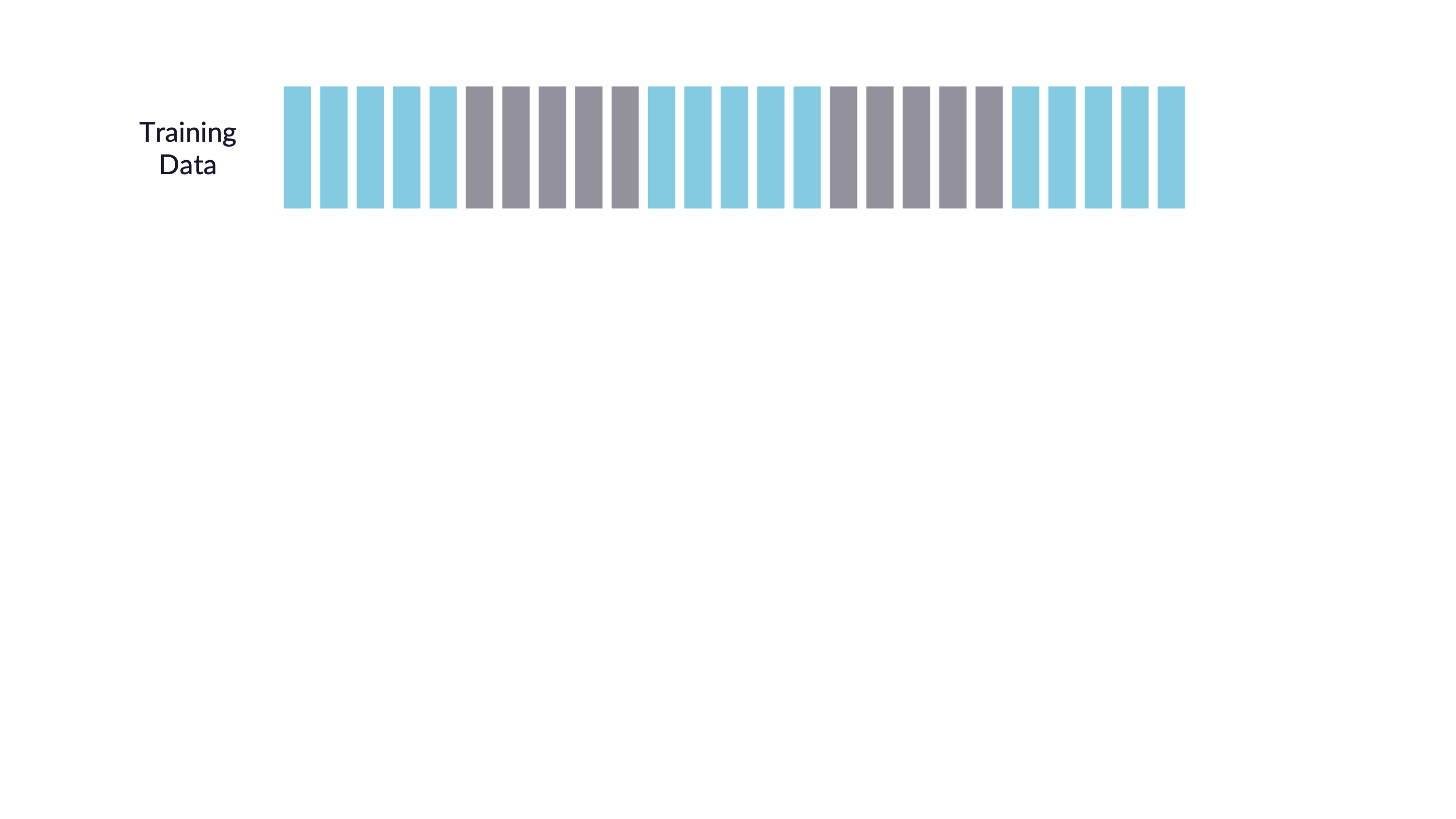
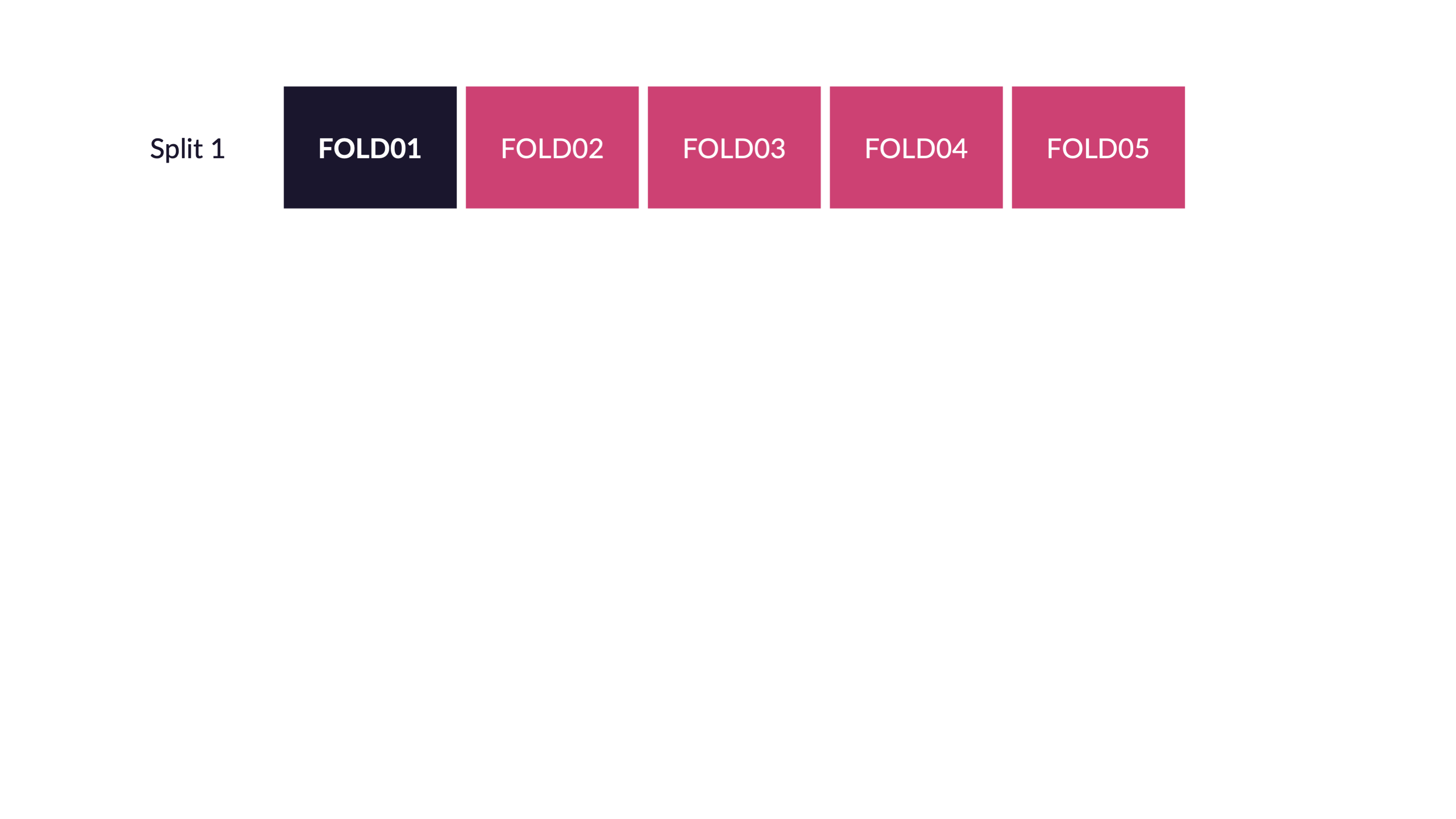
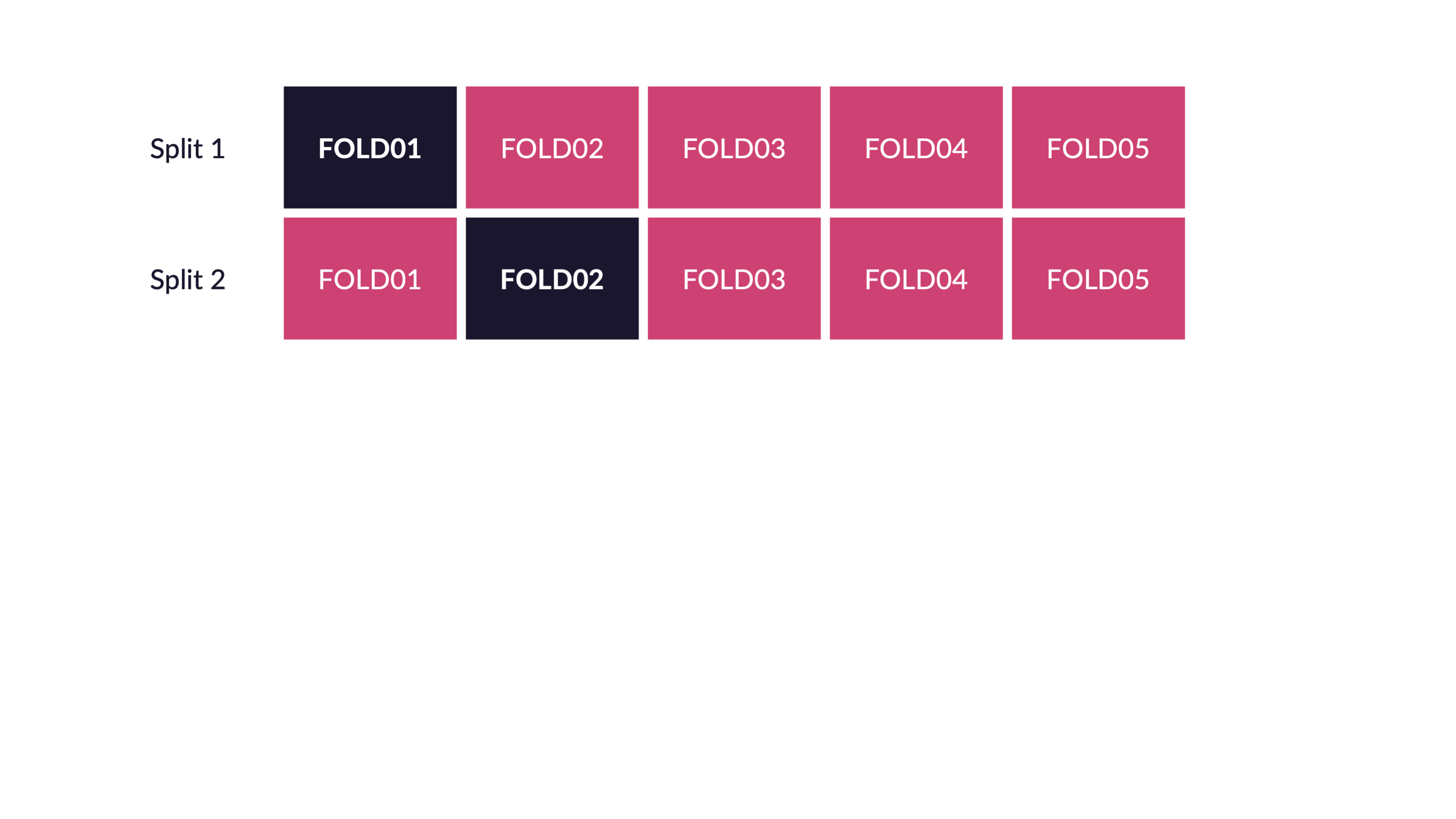
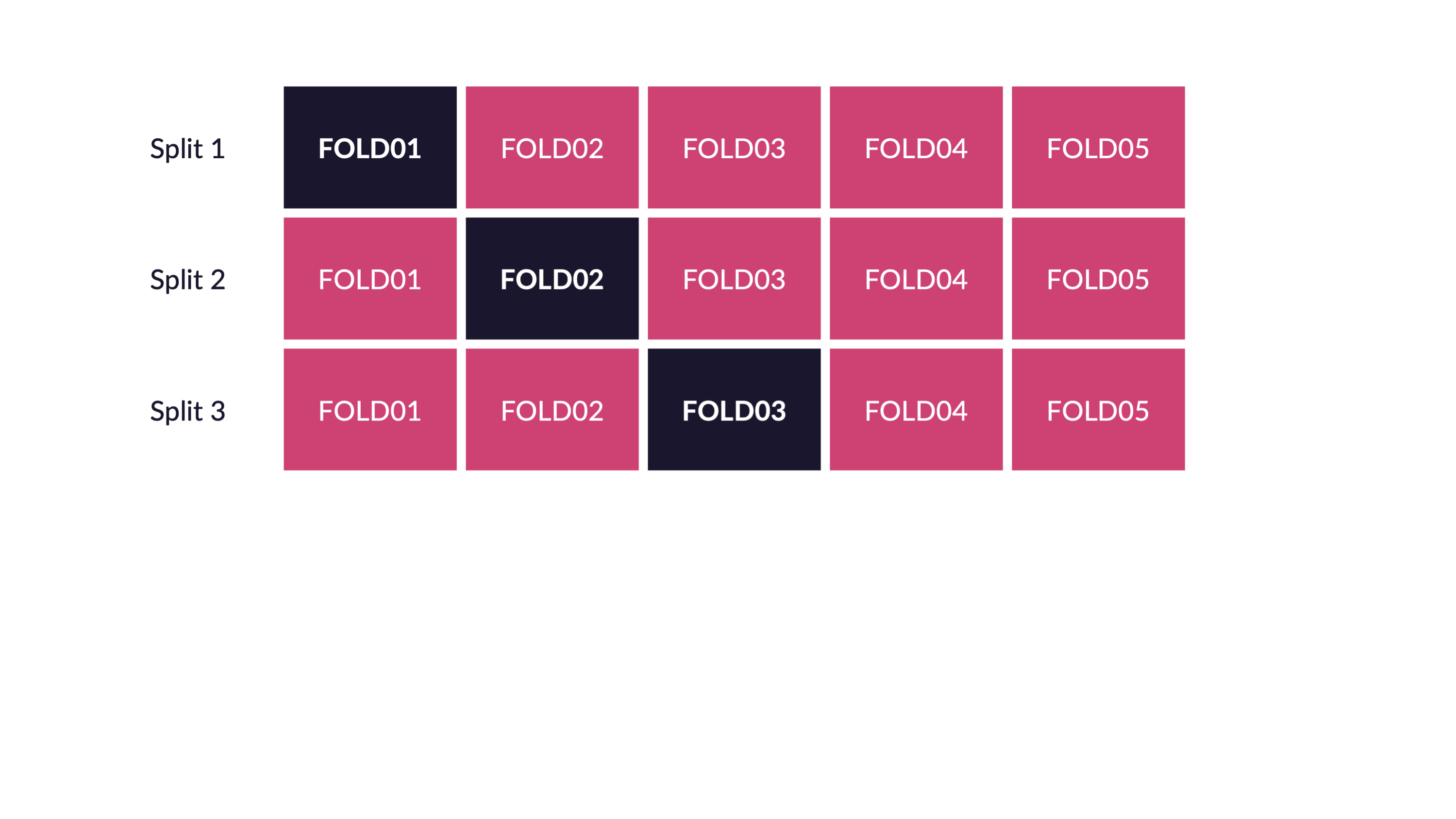
$V$-fold cross-validation

Fit $V$ models, each on $V-1$ folds
Evaluate each model on the held-out fold
Average the assessment metrics across the $V$ models

Each observation is used $V-1$ times for training, and once for testing

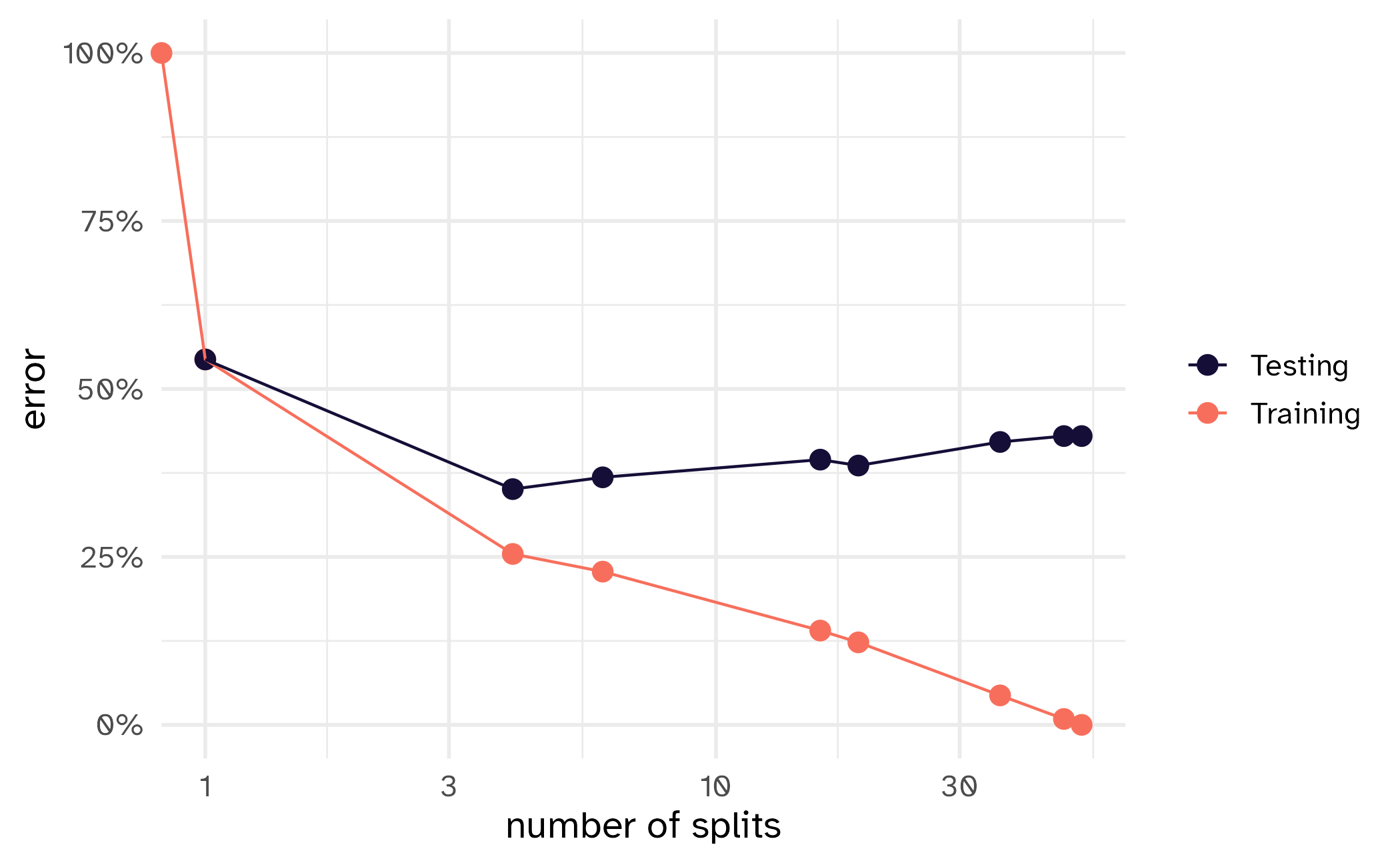
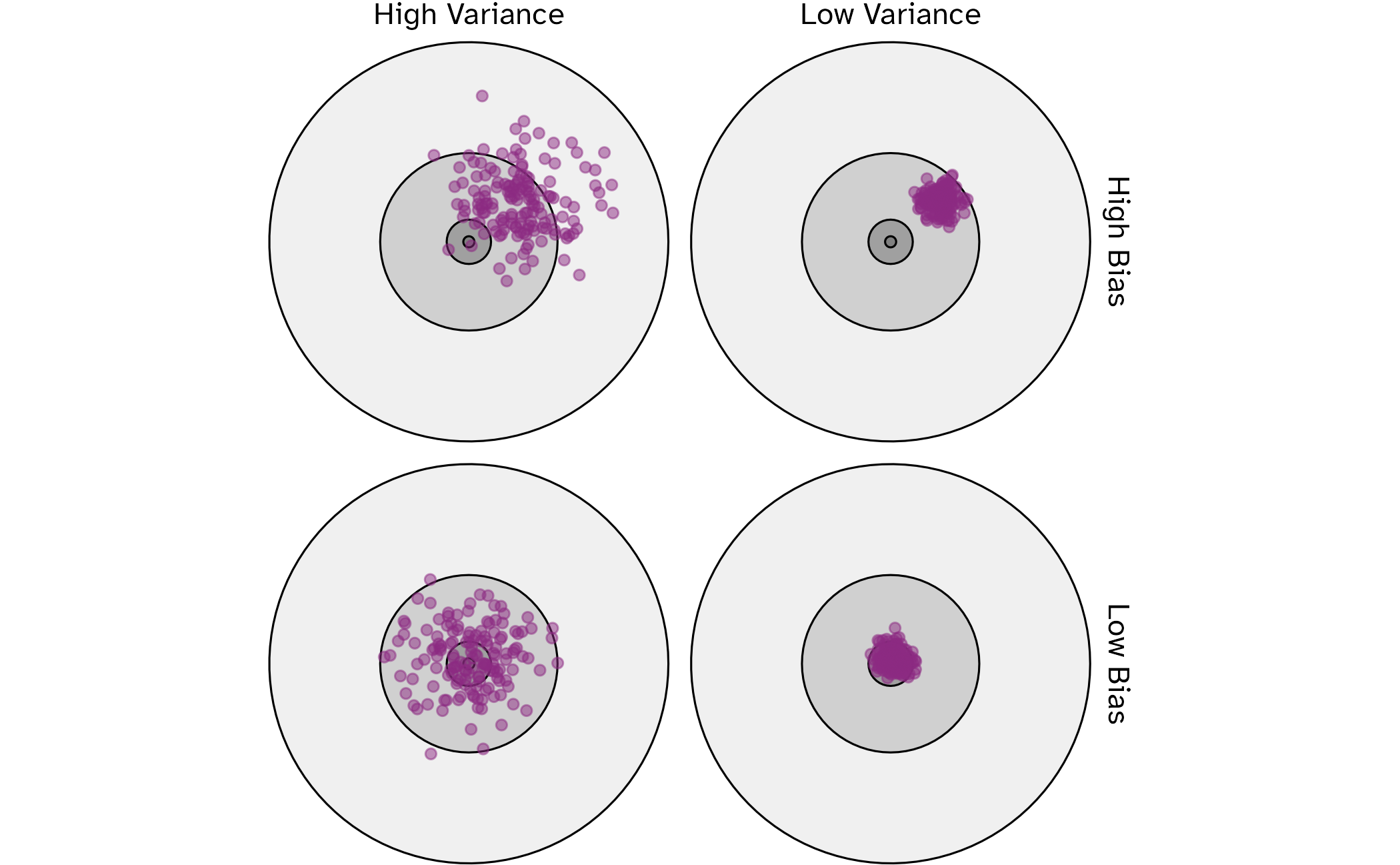
Bias vs variance

📝 Cross-validation trade-offs

Instructions

You have a dataset with 1,000 observations and are deciding between 5-fold CV and 10-fold CV. For each approach, explain:

How many observations will be in each analysis set?
How many observations will be in each assessment set?
Which approach would likely give you a less biased estimate of model performance?
Which approach would likely give you more stable (less variable) results?
Which would you choose and why?

05:00

Selecting $V$

As $V$ increases, bias decreases and variance increases
As $V$ decreases, bias increases and variance decreases
Computation time goes up with $V$

Common choices are $V=5$ or $V=10$

Cross-validation extensions

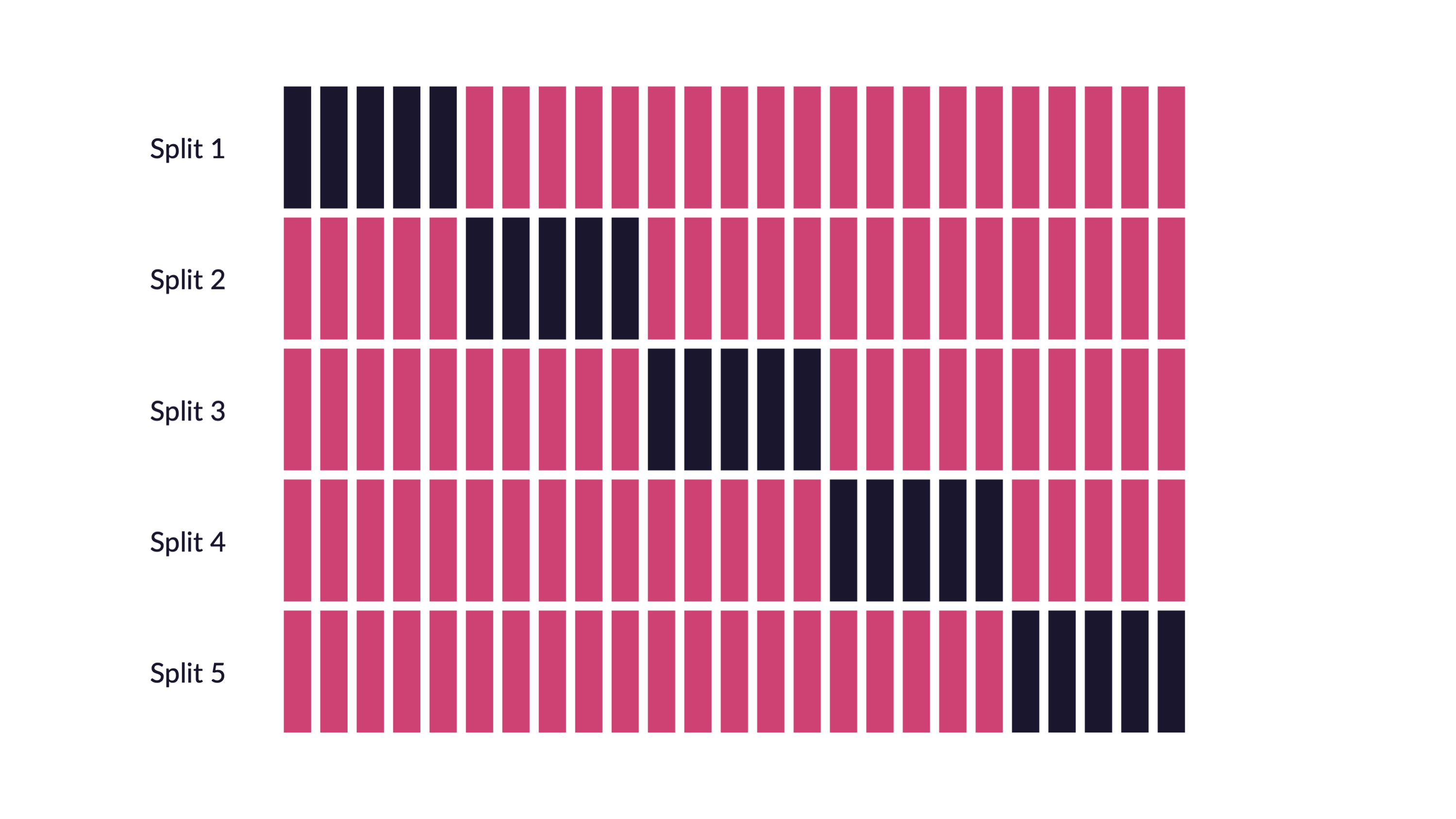
Repeated cross-validation: repeat the $V$-fold CV process multiple times with different random splits
- Reduces variance of $V$-fold CV by generating more resamples to average
Monte Carlo cross-validation: randomly partition fixed $p$ proportion of data into assessment set, but use random sampling for each fold
- Some observations may be used multiple times in the assessment set, while others may never be used
- Potentially better for smaller datasets
Spatial cross-validation: create folds based on spatial location to account for spatial autocorrelation

Validation sets

Used when

Original data set is very large
Model training is very computationally expensive (e.g., deep learning)

Bootstrap resampling

Rarely used for ML model assessment, but core method for statistical inference and ensemble methods (e.g., bagging, random forests)

Rolling forecasting origin resampling

Preserves temporal ordering of observations for time series data

How to use resampling in ML workflows

Estimating model performance

For each $B$ resample:

Use the analysis set to perform all model training actions, including:
- Preprocess the data
- Apply preprocessing steps to itself
- Fit the model
Use the assessment set to perform all model evaluation actions, including:
- Apply the preprocessing steps learned from the analysis set to the assessment set
- Generate predictions
- Calculate performance metrics

Average the performance metrics across the $B$ models

Do I need to generate new resamples for each model?

How do I get consistently random partitions?

Random number generators (RNGs)
Set a random seed before partitioning

R
Python

set.seed(123)

# built-in random module
import random
random.seed(123)

# numpy RNG
import numpy as np
np.random.seed(123)

How do I get this to run faster?

Embarrassingly parallel computations

Use parallel processing to estimate models independently across resamples

Limited only by available hardware resources (CPU cores, RAM, etc.)

R
Python

# with {future}
library(future)
plan("multisession")

# with {mirai}
library(future)
plan("multisession")

Use the n_jobs parameter in sklearn.model_selection.cross_validate() (and comparable functions)

Resampling with {tidymodels}

Partition into training/test sets

library(tidymodels)
set.seed(123)

penguins_split <- initial_split(data = penguins, prop = 0.7)
penguins_split

<Training/Testing/Total>
<233/100/333>

Partition into training/test sets

penguins_train <- training(penguins_split)
penguins_test <- testing(penguins_split)

penguins_train

# A tibble: 233 × 8
   species   island    bill_len bill_dep flipper_len body_mass sex     year
   <fct>     <fct>        <dbl>    <dbl>       <int>     <int> <fct>  <int>
 1 Gentoo    Biscoe        59.6     17           230      6050 male    2007
 2 Adelie    Torgersen     34.4     18.4         184      3325 female  2007
 3 Gentoo    Biscoe        45.2     15.8         215      5300 male    2008
 4 Chinstrap Dream         49       19.5         210      3950 male    2008
 5 Adelie    Torgersen     41.4     18.5         202      3875 male    2009
 6 Chinstrap Dream         51       18.8         203      4100 male    2008
 7 Gentoo    Biscoe        44.9     13.8         212      4750 female  2009
 8 Gentoo    Biscoe        51.1     16.5         225      5250 male    2009
 9 Chinstrap Dream         50.8     19           210      4100 male    2009
10 Gentoo    Biscoe        45.4     14.6         211      4800 female  2007
# ℹ 223 more rows

penguins_test

# A tibble: 100 × 8
   species island    bill_len bill_dep flipper_len body_mass sex     year
   <fct>   <fct>        <dbl>    <dbl>       <int>     <int> <fct>  <int>
 1 Adelie  Torgersen     39.5     17.4         186      3800 female  2007
 2 Adelie  Torgersen     40.3     18           195      3250 female  2007
 3 Adelie  Torgersen     38.7     19           195      3450 female  2007
 4 Adelie  Torgersen     46       21.5         194      4200 male    2007
 5 Adelie  Biscoe        35.9     19.2         189      3800 female  2007
 6 Adelie  Biscoe        38.2     18.1         185      3950 male    2007
 7 Adelie  Dream         39.5     17.8         188      3300 female  2007
 8 Adelie  Dream         36       18.5         186      3100 female  2007
 9 Adelie  Dream         42.3     21.2         191      4150 male    2007
10 Adelie  Biscoe        39.6     17.7         186      3500 female  2008
# ℹ 90 more rows

Resample the training set

penguins_folds <- vfold_cv(penguins_train, v = 5, repeats = 5)
penguins_folds

#  5-fold cross-validation repeated 5 times 
# A tibble: 25 × 3
   splits           id      id2  
   <list>           <chr>   <chr>
 1 <split [186/47]> Repeat1 Fold1
 2 <split [186/47]> Repeat1 Fold2
 3 <split [186/47]> Repeat1 Fold3
 4 <split [187/46]> Repeat1 Fold4
 5 <split [187/46]> Repeat1 Fold5
 6 <split [186/47]> Repeat2 Fold1
 7 <split [186/47]> Repeat2 Fold2
 8 <split [186/47]> Repeat2 Fold3
 9 <split [187/46]> Repeat2 Fold4
10 <split [187/46]> Repeat2 Fold5
# ℹ 15 more rows

Fit model to each resample

knn_mod <- nearest_neighbor(neighbors = 5) |>
  set_engine("kknn") |>
  set_mode("regression")

knn_mod |>
  fit_resamples(
    preprocessor = body_mass ~ .,
    resamples = penguins_folds
  ) |>
  collect_metrics()

# A tibble: 2 × 6
  .metric .estimator    mean     n std_err .config             
  <chr>   <chr>        <dbl> <int>   <dbl> <chr>               
1 rmse    standard   321.       25 5.16    Preprocessor1_Model1
2 rsq     standard     0.847    25 0.00600 Preprocessor1_Model1

Fit model to each resample

tree_mod <- decision_tree() |>
  set_engine("rpart") |>
  set_mode("regression")

tree_mod |>
  fit_resamples(
    preprocessor = body_mass ~ .,
    resamples = penguins_folds
  ) |>
  collect_metrics()

# A tibble: 2 × 6
  .metric .estimator    mean     n std_err .config             
  <chr>   <chr>        <dbl> <int>   <dbl> <chr>               
1 rmse    standard   329.       25 8.06    Preprocessor1_Model1
2 rsq     standard     0.839    25 0.00866 Preprocessor1_Model1

Resampling with `scikit-learn`

Partition into training/test sets

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, RepeatedKFold, cross_validate
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error, r2_score
from palmerpenguins import load_penguins

np.random.seed(123)

penguins = load_penguins().dropna()

X = penguins.drop(["body_mass_g", "species", "island", "sex"], axis=1)
y = penguins["body_mass_g"]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3
)

X_train.shape

(233, 4)

X_test.shape

(100, 4)

Resample the training set

cv = RepeatedKFold(n_splits=5, n_repeats=5)

cv.get_n_splits()

Fit model to each resample

knn_model = KNeighborsRegressor(n_neighbors=5)

knn_cv_results = cross_validate(
    estimator=knn_model,
    X=X_train,
    y=y_train,
    cv=cv,
    scoring={"neg_root_mean_squared_error": "neg_root_mean_squared_error", "r2": "r2"},
    return_train_score=False,
)

knn_rmse_scores = -knn_cv_results["test_neg_root_mean_squared_error"]
knn_r2_scores = knn_cv_results["test_r2"]

knn_metrics = pd.DataFrame(
    {
        "metric": ["rmse", "rsq"],
        "estimator": ["standard", "standard"],
        "mean": [knn_rmse_scores.mean(), knn_r2_scores.mean()],
        "n": [len(knn_rmse_scores), len(knn_r2_scores)],
        "std_err": [
            knn_rmse_scores.std() / np.sqrt(len(knn_rmse_scores)),
            knn_r2_scores.std() / np.sqrt(len(knn_r2_scores)),
        ],
    }
)

knn_metrics

  metric estimator        mean   n   std_err
0   rmse  standard  348.551212  25  5.207057
1    rsq  standard    0.799162  25  0.008655

Fit model to each resample

tree_model = DecisionTreeRegressor()

tree_cv_results = cross_validate(
    estimator=tree_model,
    X=X_train,
    y=y_train,
    cv=cv,
    scoring={"neg_root_mean_squared_error": "neg_root_mean_squared_error", "r2": "r2"},
    return_train_score=False,
)

tree_rmse_scores = -tree_cv_results["test_neg_root_mean_squared_error"]
tree_r2_scores = tree_cv_results["test_r2"]

tree_metrics = pd.DataFrame(
    {
        "metric": ["rmse", "rsq"],
        "estimator": ["standard", "standard"],
        "mean": [tree_rmse_scores.mean(), tree_r2_scores.mean()],
        "n": [len(tree_rmse_scores), len(tree_r2_scores)],
        "std_err": [
            tree_rmse_scores.std() / np.sqrt(len(tree_rmse_scores)),
            tree_r2_scores.std() / np.sqrt(len(tree_r2_scores)),
        ],
    }
)

tree_metrics

  metric estimator        mean   n    std_err
0   rmse  standard  470.879978  25  11.425615
1    rsq  standard    0.633047  25   0.018241

Wrap-up

Recap

Data partitioning is essential to avoid overfitting and ensure reliable model evaluation
Resampling methods like cross-validation help estimate model performance while minimizing bias
Avoid information leakage by carefully timing data splits and preprocessing steps

Use your data

Announcements

Announcements

Learning objectives

Why partition data?

Data splitting and spending

Meet the Palmer penguins

penguins

How might we spend our data?

Simple data partitioning

The holdout method

How do we split?

Simple random sampling

📝 Is simple random sampling appropriate?

Information leakage

📝 Preventing information leakage

Using the training set

Resampling methods

Data Splitting

Resampling methods

\(V\)-fold cross-validation

\(V\)-fold cross-validation

Bias vs variance

📝 Cross-validation trade-offs

Selecting \(V\)

Cross-validation extensions

Validation sets

Bootstrap resampling

Rolling forecasting origin resampling

How to use resampling in ML workflows

Estimating model performance

Do I need to generate new resamples for each model?

How do I get consistently random partitions?

How do I get this to run faster?

Resampling with {tidymodels}

Partition into training/test sets

Partition into training/test sets

Resample the training set

Fit model to each resample

Fit model to each resample

Resampling with scikit-learn

Partition into training/test sets

Resample the training set

Fit model to each resample

Fit model to each resample

Wrap-up

Recap

`penguins`

Resampling with `scikit-learn`