Build better data (II)

Lecture 6

Dr. Benjamin Soltoff

Cornell University
INFO 4940/5940 - Fall 2025

September 11, 2025

Announcements

Homework 02

Learning objectives

Identify potential issues with numeric predictors
Implement transformation methods to mitigate issues with numeric predictors
Identify the importance of interaction terms in predictive models
Introduce non-linear transformations for numeric predictors
Model interactive and non-linear relationships between predictors and the response variable

Problems with numeric predictors

Potential issues with numeric predictors

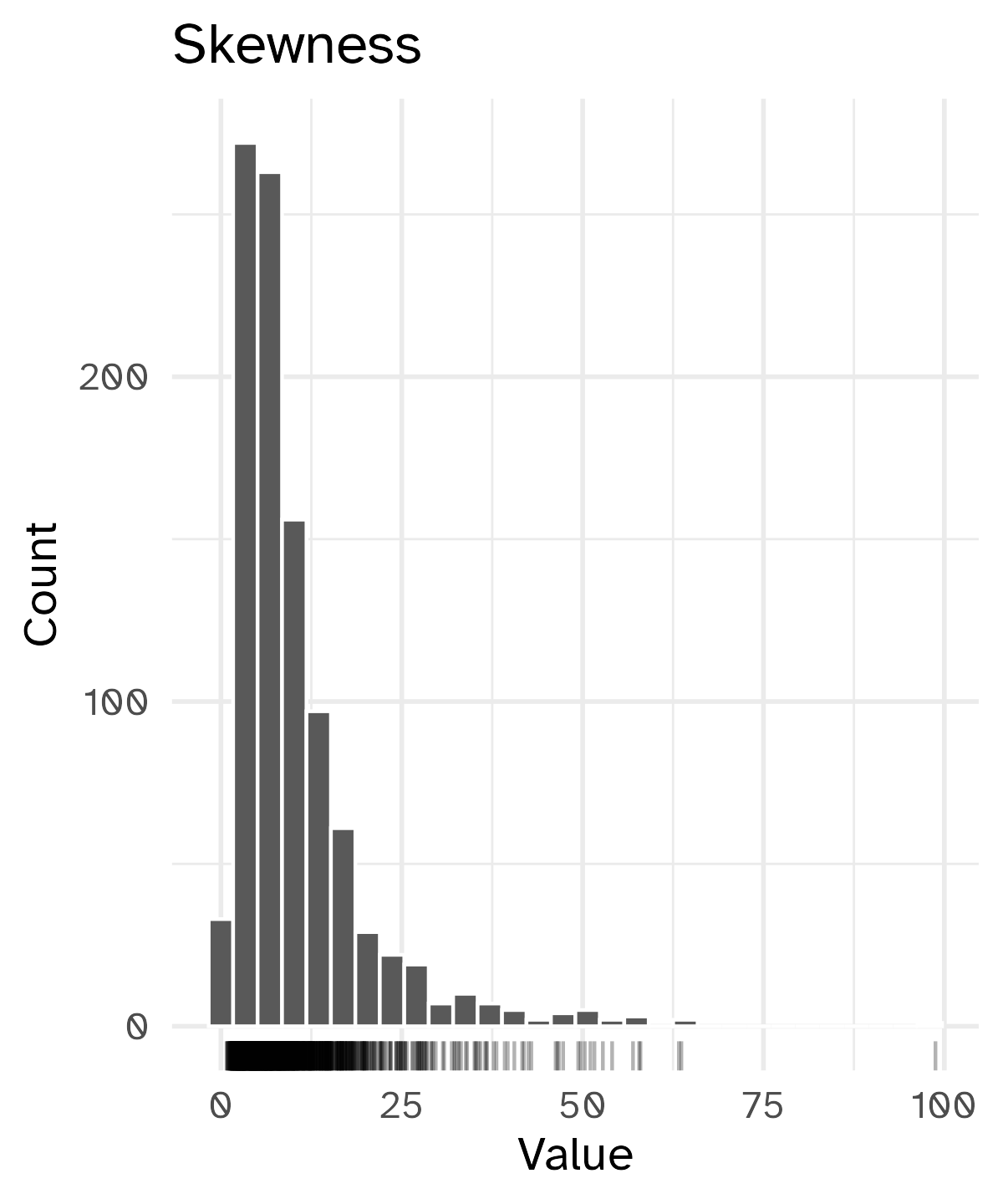
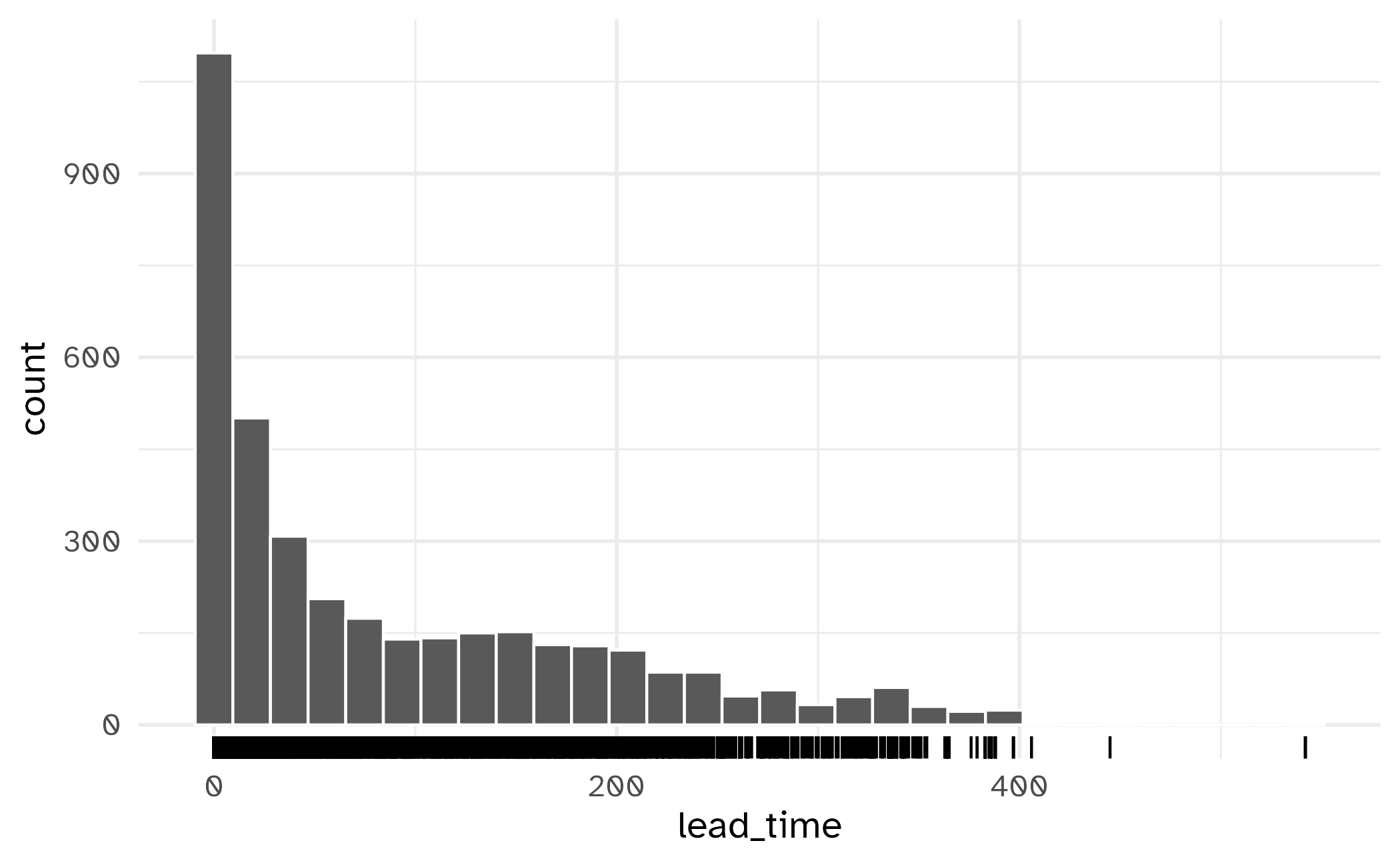
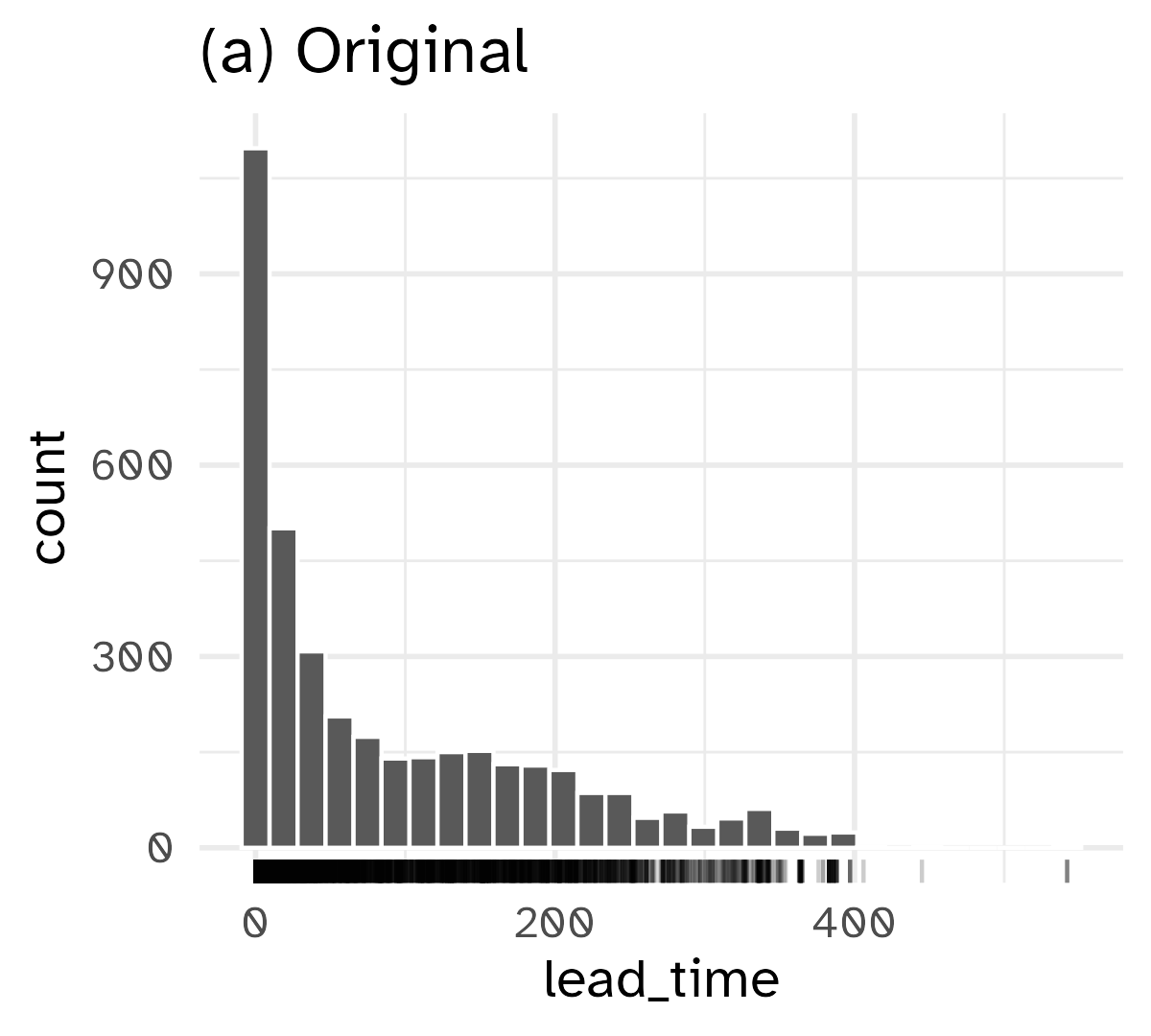
Skewed variables

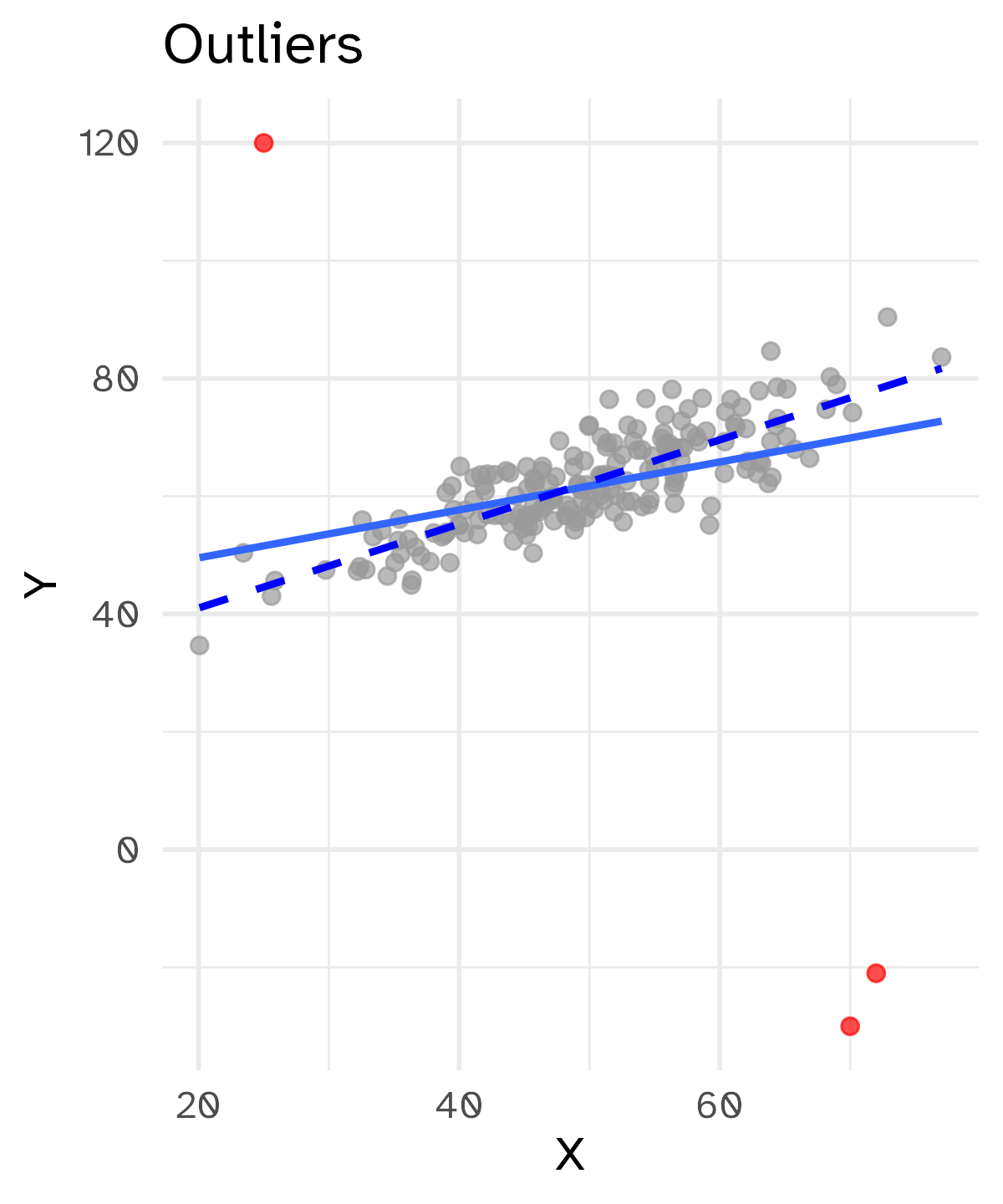
Outliers

Something (such as a geologic feature) that is situated away from or classed differently from a main or related body.¹

A statistical observation that is markedly different in value from the others of the sample.²

Extreme values are not inherently “wrong”. Removing them can also skew our analysis by excluding relevant data points.

But we also do not want to give abnormal weight to these outliers.

📝 What to do with outliers?

Instructions

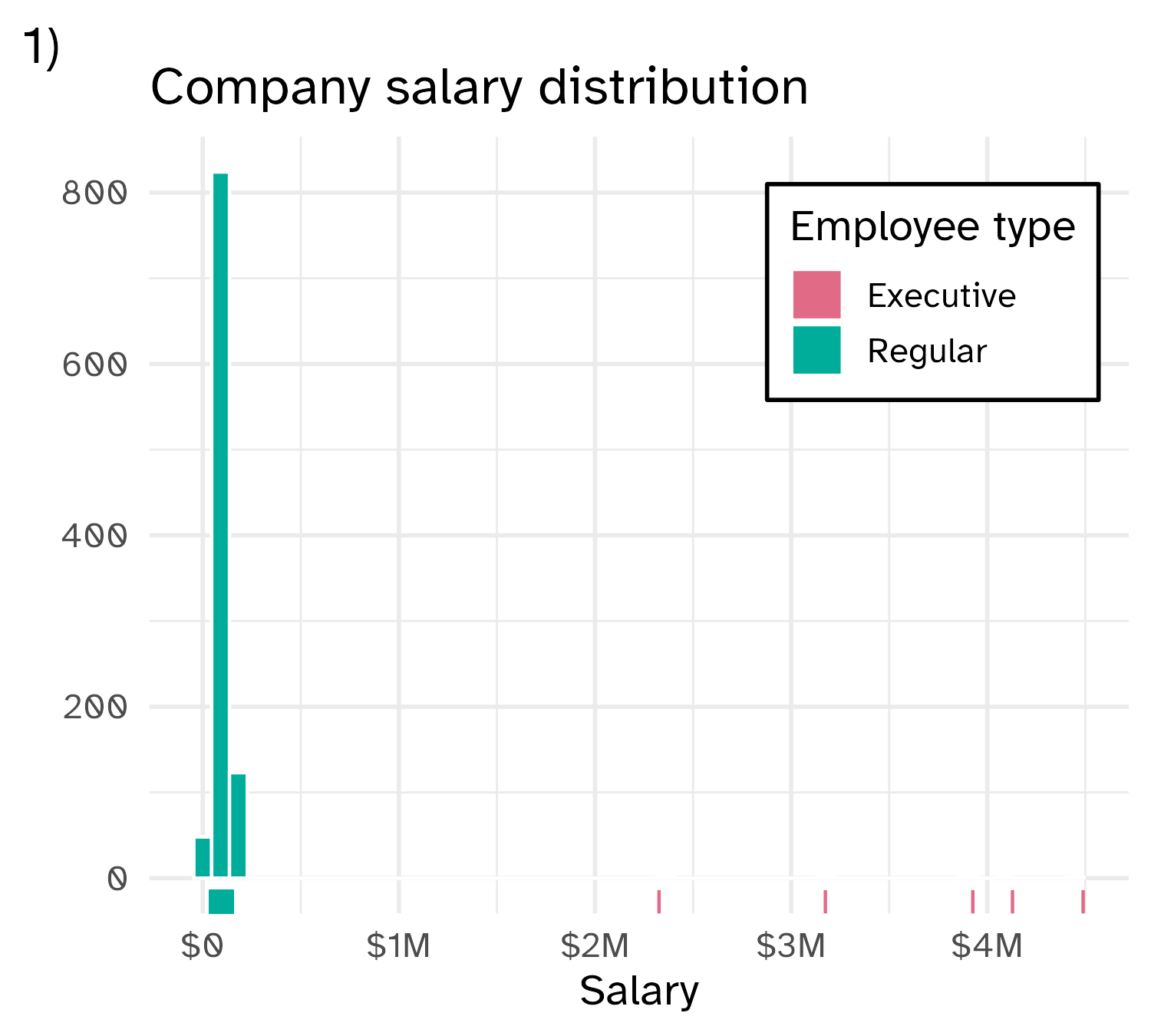
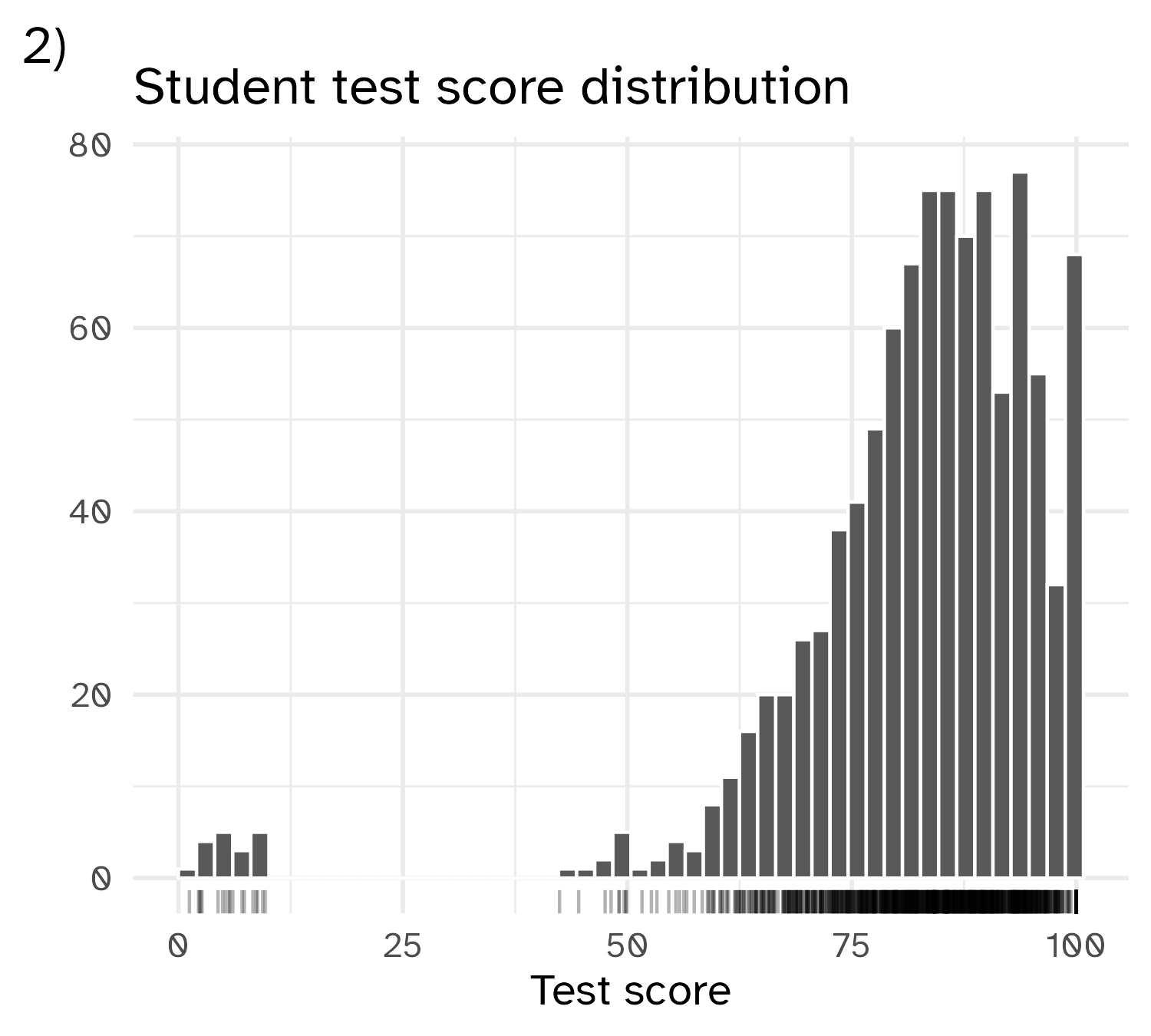
Options

Keep as-is
Remove completely
Cap/truncate values
Transform the variable

07:00

1 : 1 transformations

One-to-one functional transformation of a single predictor $x$ to a new predictor $x^*$

\[ x^* = f(x) \]

Preserve relative ordering of values while resolving asymmetry or skewness

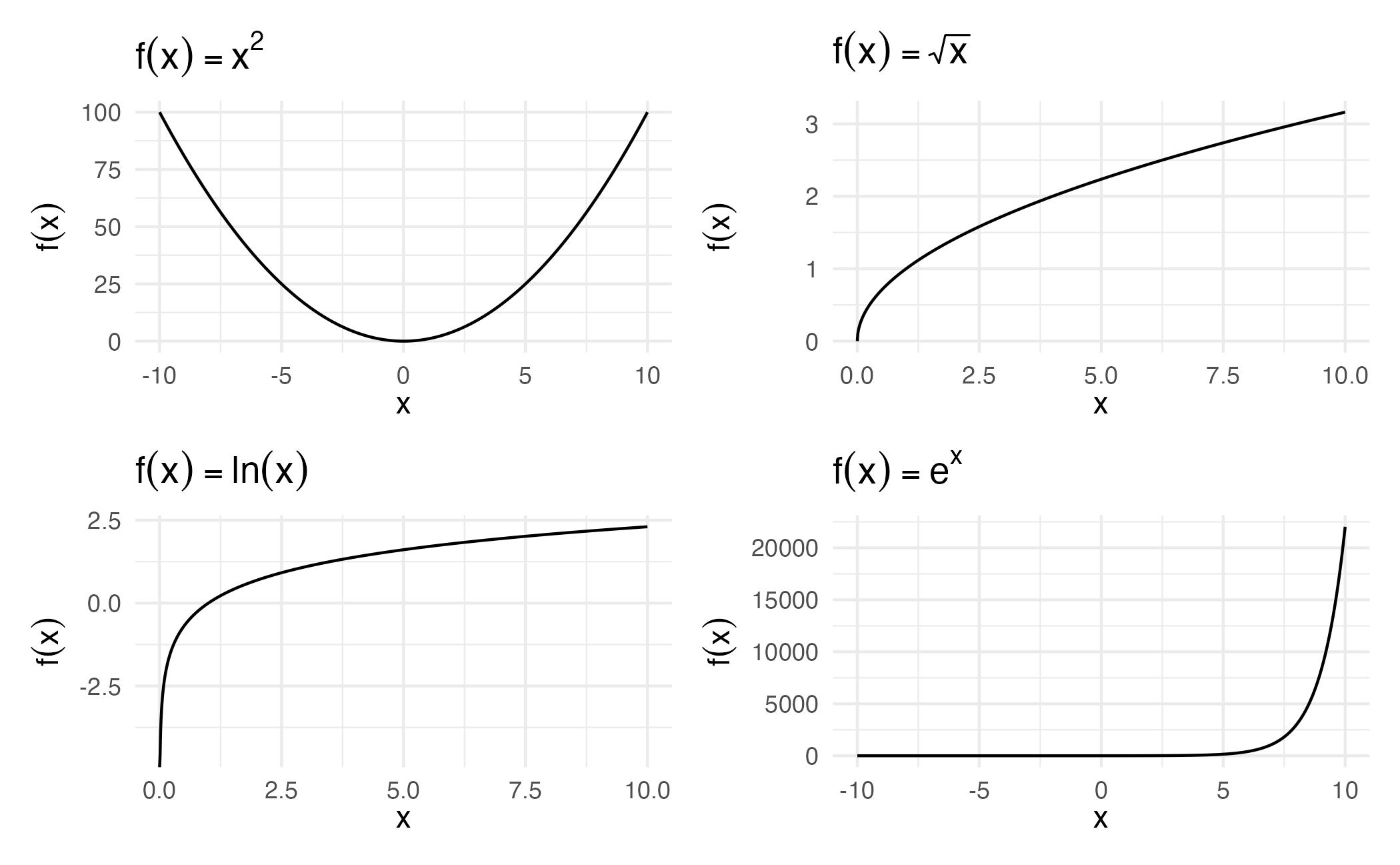
Transformation functions

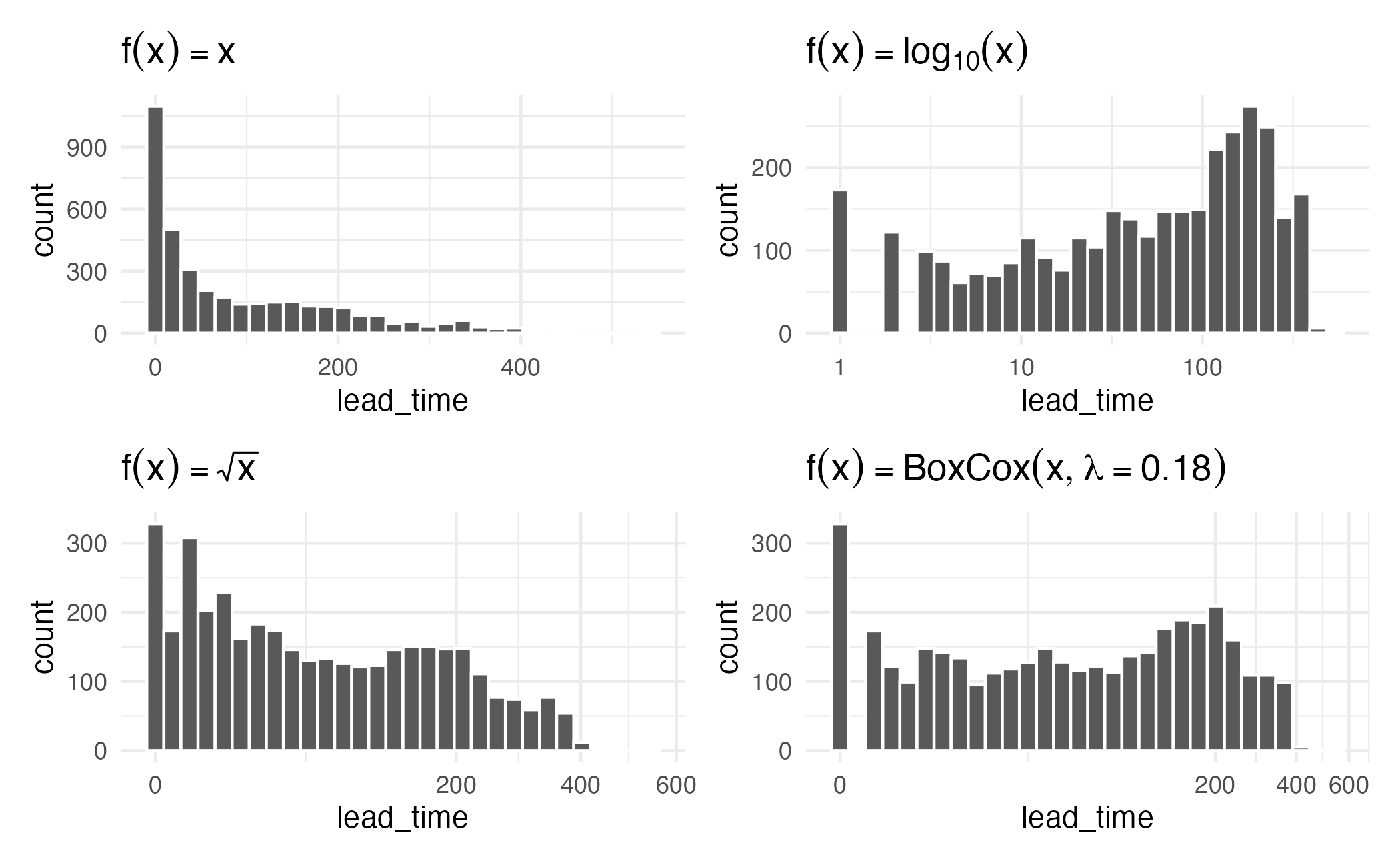
Box-Cox procedure

\[ x^* = \begin{cases} \lambda^{-1}(x^\lambda-1) & \text{if $\lambda \ne 0$,} \\[3pt] \log(x) &\text{if $\lambda = 0$.} \end{cases} \]

Box-Cox procedure

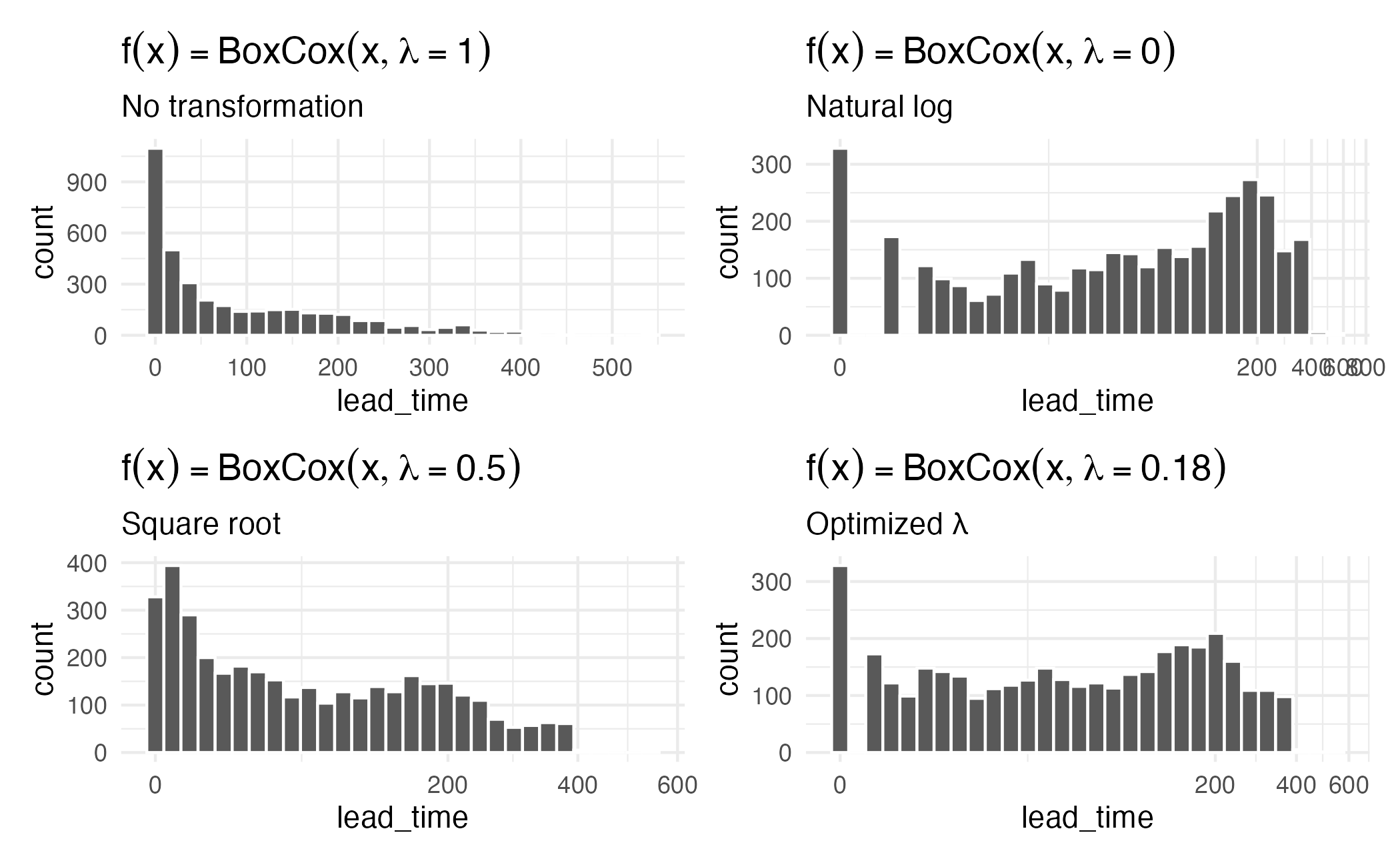
Yeo-Johnson

Box-Cox transformations only work on positive values
Yeo-Johnson extends this to work with all numeric values

\[ x^* = \begin{cases} \lambda^{-1}\left[(x + 1)^\lambda-1\right] & \text{if $\lambda \ne 0$ and $x \ge 0$,} \\[3pt] \log(x + 1) &\text{if $\lambda = 0$ and $x \ge 0$.} \\[3pt] -(2 - \lambda)^{-1}\left[(-x + 1)^{2 - \lambda}-1\right] & \text{if $\lambda \ne 2$ and $x < 0$,} \\[3pt] -\log(-x + 1) &\text{if $\lambda = 2$ and $x < 0$.} \end{cases} \]

How is $\lambda$ determined?

$\lambda$ is a parameter to be learned from the data - what value of $\lambda$ results in the best approximation to a normal distribution?

# A tibble: 1 × 3
  terms     value id              
  <chr>     <dbl> <chr>           
1 lead_time 0.178 YeoJohnson_FgnP3

Training data used to estimate model parameters
Training data used to estimate transformation parameters

Result of transformation

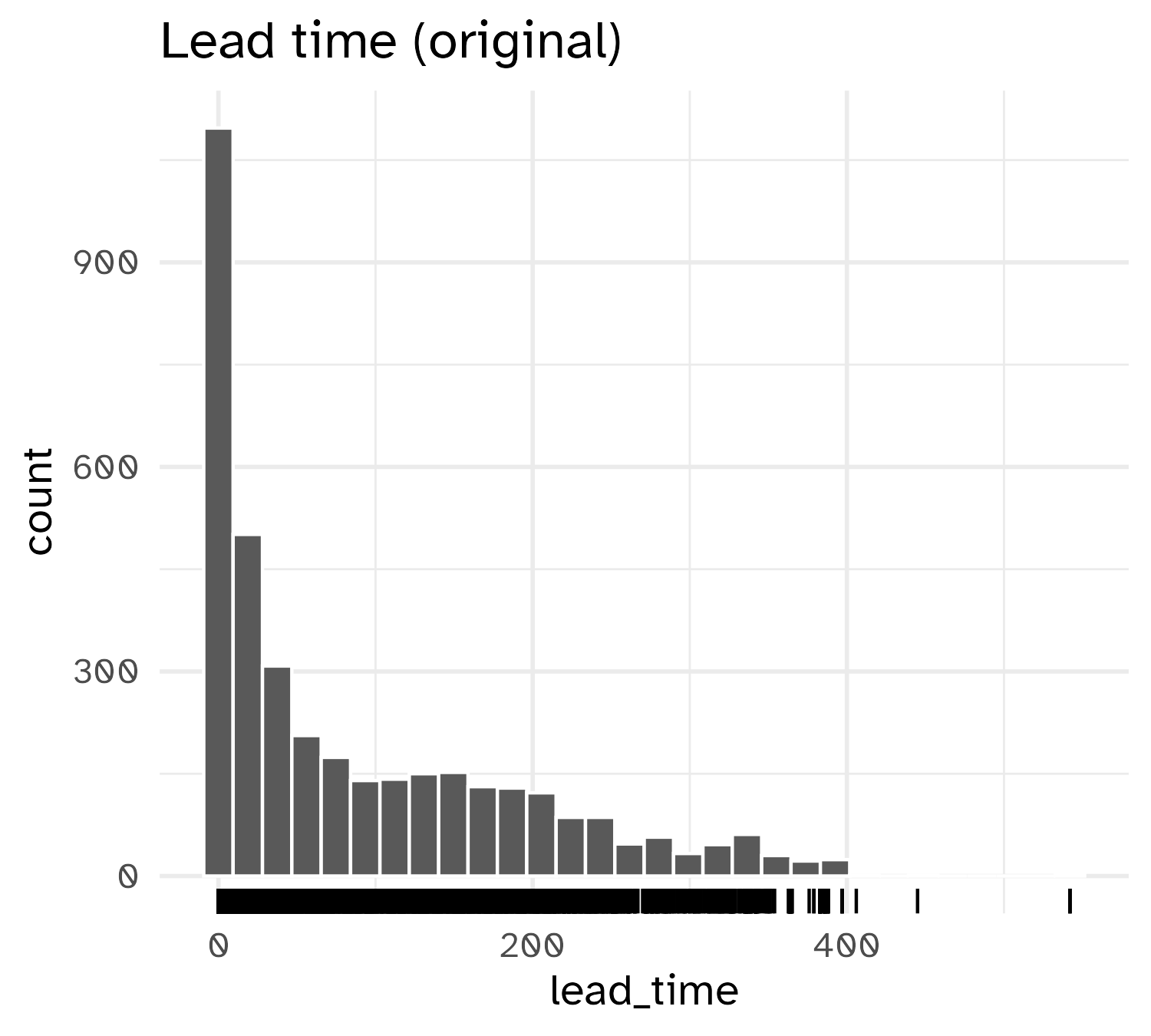
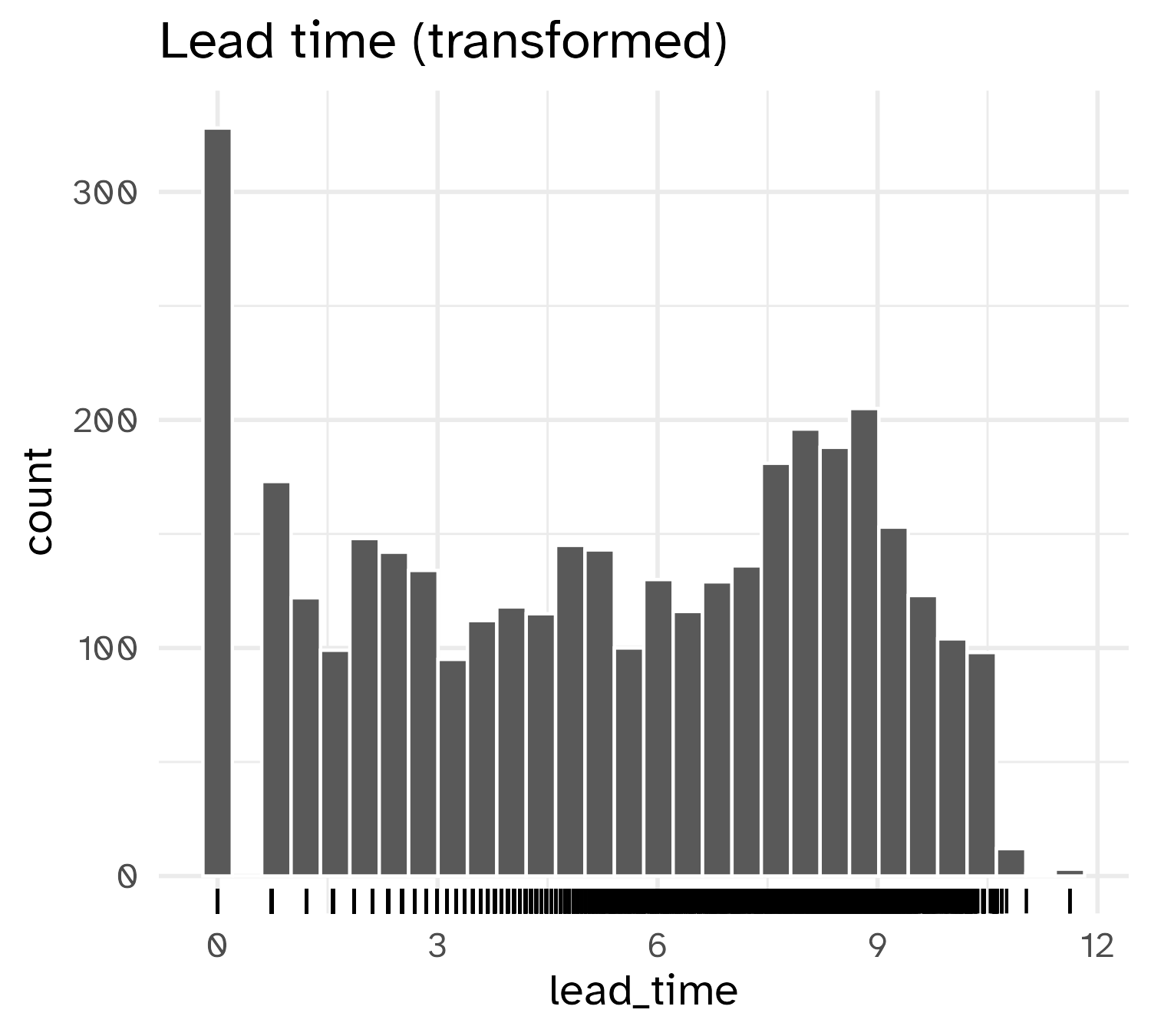
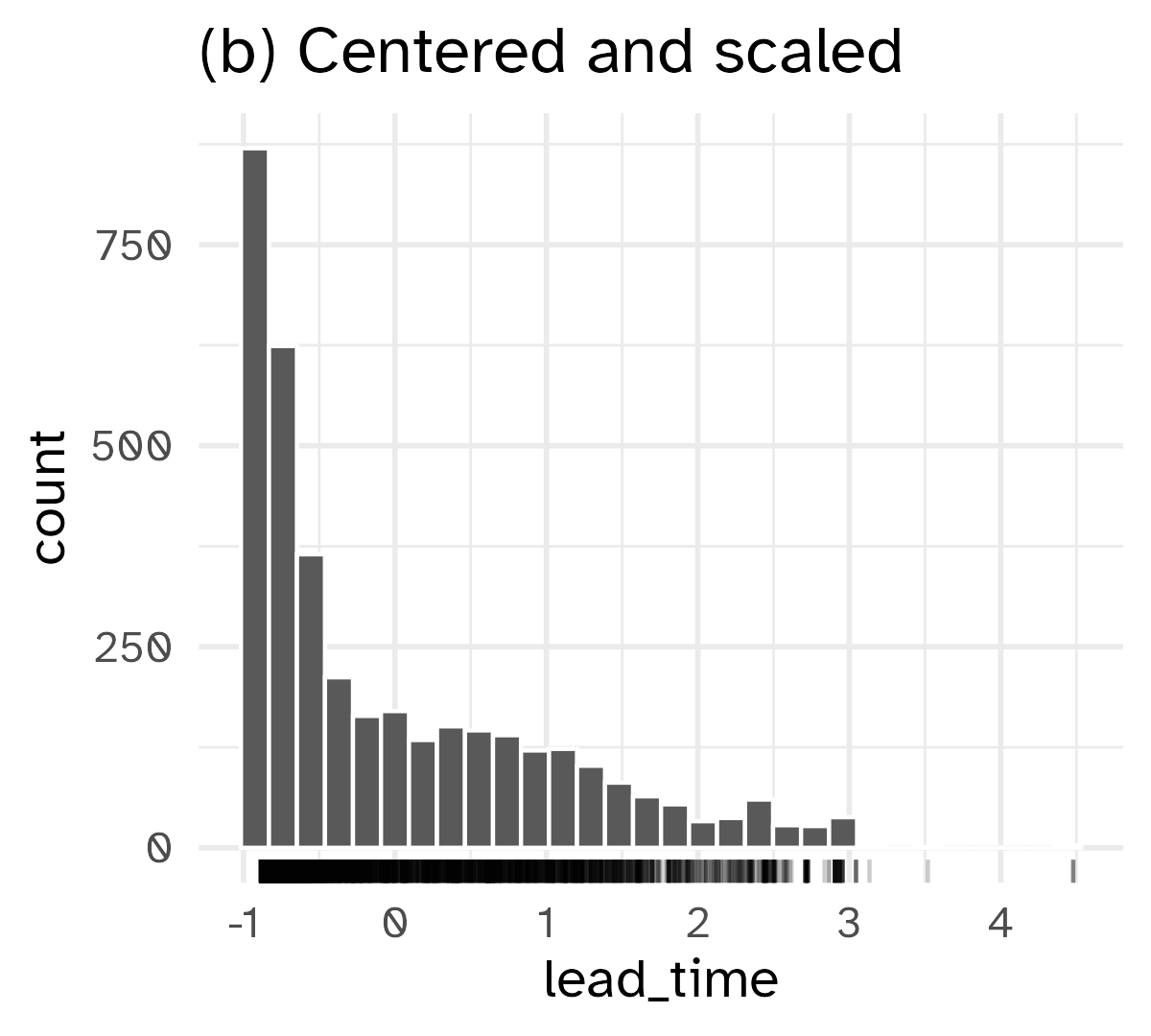
Standardizing to a common scale

Some models require predictors to be on a common scale (data preprocessing)

$k$ nearest neighbors
Support vector machines
Penalized regression

Normalization

\[ x^* = \frac{x - \bar{x}}{\widehat{\text{sd}(x)}} \]

Use the training set (analysis set) to estimate $\bar{x}$ and $\widehat{\text{sd}(x)}$
Apply the same transformation to the test set (assessment set)

Standardizing to a common scale

Interactions

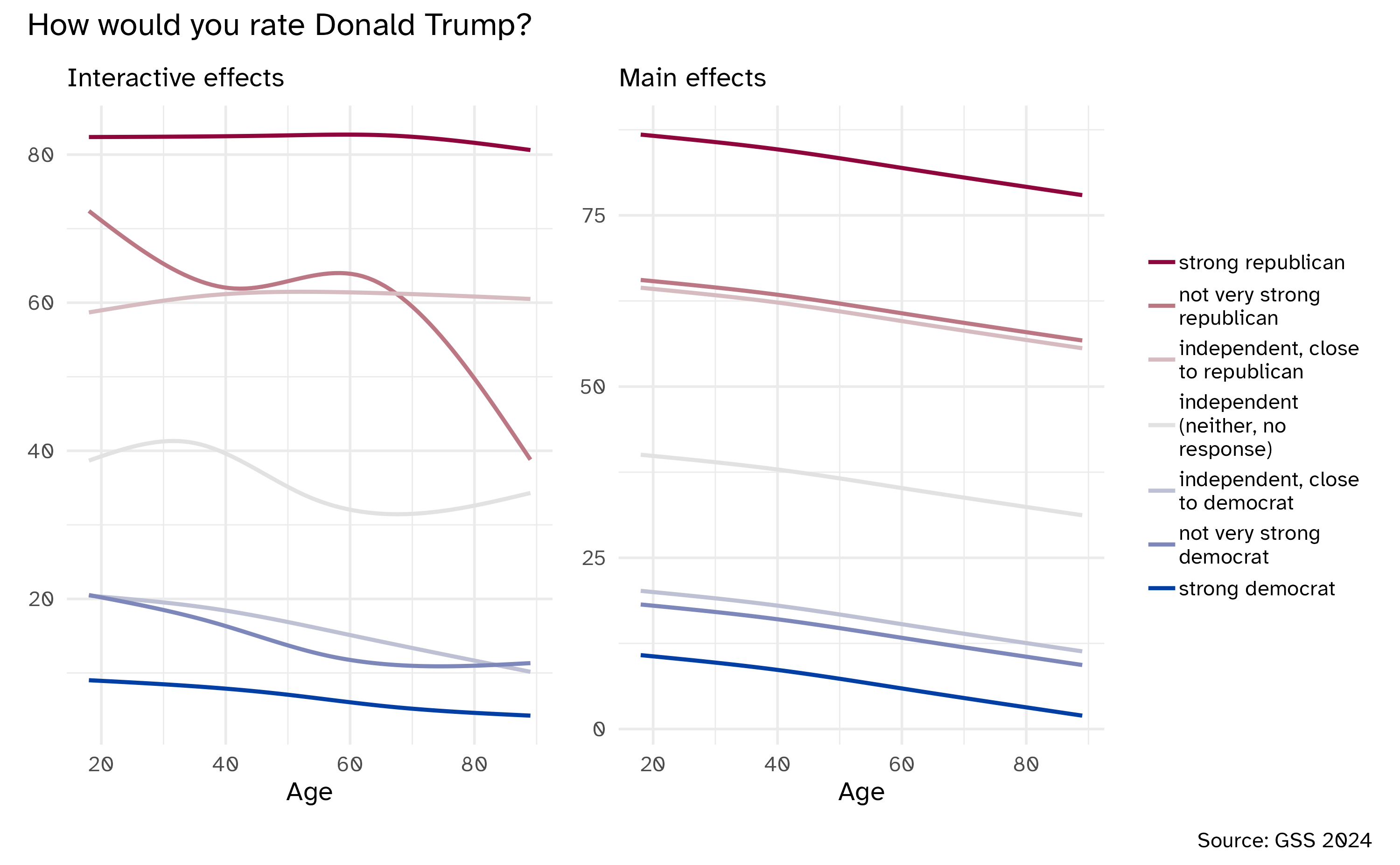
Interactive effects

\[ \Large{\hat{Y} = b_0 + b_1 X_1 + b_2 X_2 + b_3 X_3 + \ldots} \]

Assumes a linear, additive relationship between $X_i$ and $Y$

What if effects are interactive?

Temperature and humidity on energy consumption
Drug dosage and age on treatment effectiveness
Age and income on spending

Incorporating interactive effects

Add a product term to the model

\[ \Large{\hat{Y} = b_0 + b_1 X_1 + b_2 X_2 + b_3 \times X_1 \times X_2} \]

Interpreting interactive terms

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| label: shiny-interaction-contours
#| viewerHeight: 700
#| viewerWidth: "100%"
#| standalone: true

library(shiny)
library(ggplot2)
library(bslib)
library(viridis)
library(scales)
library(colorspace)

light_bg <- "#fcfefe" # from aml4td.scss
grid_theme <- bs_theme(
  bg = light_bg,
  fg = "#595959"
)

theme_light_bl <- function(...) {
  ret <- ggplot2::theme_bw(...)

  col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)
  ret$panel.background <- col_rect
  ret$plot.background <- col_rect
  ret$legend.background <- col_rect
  ret$legend.key <- col_rect

  ret$legend.position <- "top"

  ret
}

ui <- page_fillable(
  theme = bs_theme(bg = "#fcfefe", fg = "#595959"),
  padding = "1rem",
  tags$head(
    tags$style(
      type = 'text/css',
      '.irs-grid-text {font-size: 20px;}', # For grid values (min, max, ticks)
      '.irs-single {font-size: 24px;}' # For the currently selected value on the handle
    )
  ),
  layout_columns(
    card(
      sliderInput(
        "beta_1",
        label = "Predictor 1 slope",
        min = -4.0,
        max = 4.0,
        step = 0.5,
        value = 1
      ),
      sliderInput(
        "beta_2",
        label = "Predictor 2 slope",
        min = -4.0,
        max = 4.0,
        step = 0.5,
        value = 1
      ),
      sliderInput(
        "beta_int",
        label = "Interaction slope",
        min = -2.0,
        max = 2.0,
        step = 0.25,
        value = 0.5
      )
    ),
    plotOutput("contours")
  ),
  as_fill_carrier()
)

server <- function(input, output) {
  # ------------------------------------------------------------------------------

  n_grid <- 100
  grid_1d <- seq(-2, 2, length.out = n_grid)
  grid <- expand.grid(A = grid_1d, B = grid_1d)

  output$contours <-
    renderPlot({
      grid$outcome <-
        input$beta_1 *
        grid$A +
        input$beta_2 * grid$B +
        input$beta_int * grid$A * grid$B

      p <-
        ggplot(grid, aes(A, B)) +
        coord_equal() +
        labs(x = "Predictor 1", y = "Predictor 1") +
        theme_light_bl(base_size = 16)

      if (length(unique(grid$outcome)) >= 15) {
        p <- p +
          geom_raster(
            aes(fill = scale(outcome))
          ) +
          geom_contour(
            mapping = aes(z = scale(outcome)),
            bins = 15,
            color = "black"
          ) +
          scale_fill_continuous_diverging(
            guide = guide_colorsteps(
              frame.color = "black",
              ticks.color = NA,
              barwidth = 20
            ),
            mid = 0,
            name = NULL
          ) +
          theme(legend.position = "bottom")
      }

      print(p)
    })
}

app <- shinyApp(ui, server)
app

When to include interaction terms?

Some methods capture interactions automatically

Tree-based models (e.g. decision trees, random forests, boosted trees)
Support vector machines
Neural networks

Domain knowledge
Exploratory data analysis
Statistical tests (e.g. ANOVA, H-statistic)

Still a combination of art and science

📝 Identifying interactive effects

Instructions

For each scenario, identify whether or not you suspect an interaction effect between the two predictors on the outcome. Justify your reasoning.

Hotel booking prices: Season (summer vs. winter) and hotel star rating (1-5 stars) for resort hotels in western Europe.
Student test performance: Hours of sleep and caffeine intake (0-400 mg).
Movie theater ticket sales: Day of week (weekday vs. weekend) and movie theater capacity (100-500 seats).

07:00

Non-linear features

Basis expansion

Features of a predictor $x$ derived from a set of functions $f_1(x), f_2(x), \ldots, f_i(x)$ that can be combined using a linear combination.

Essentially an interaction with itself

Polynomial expansion

Simple linear regression

\[ y_i = \beta_0 + \beta_1 x_{i} + \epsilon_i \]

Cubic polynomial expansion

\[ y_i = \beta_0 + \beta_1 x_{i} + \beta_2 x_{i}^2 + \beta_3 x_{i}^3 + \epsilon_i \]

Polynomial expansion

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| label: fig-global-polynomial
#| viewerHeight: 700
#| viewerWidth: "100%"
#| standalone: true
library(shiny)
library(patchwork)
library(dplyr)
library(tidyr)
library(ggplot2)
library(splines2)
library(bslib)
library(viridis)
library(aspline)

data(fossil)

ui <- page_fillable(
  theme = bs_theme(
    bg = "#fcfefe",
    fg = "#595959",
    base_font = "Atkinson Hyperlegible",
    font_scale = 1.5
  ),
  padding = "1rem",
  tags$head(
    tags$style(
      type = 'text/css',
      '.irs-grid-text {font-size: 20px;}', # For grid values (min, max, ticks)
      '.irs-single {font-size: 24px;}' # For the currently selected value on the handle
    )
  ),
  layout_columns(
    fill = FALSE,
    col_widths = breakpoints(sm = c(-3, 6, -3)),
    sliderInput(
      "global_deg",
      label = "Polynomial Degree",
      min = 1L,
      max = 21L,
      step = 1L,
      value = 3L,
      ticks = TRUE
    ) # sliderInput
  ), # layout_columns
  layout_columns(
    fill = FALSE,
    col_widths = breakpoints(sm = c(-1, 10, -1)),
    as_fill_carrier(plotOutput('global', height = "500px"))
  )
)


server <- function(input, output, session) {
  light_bg <- "#fcfefe" # from aml4td.scss
  grid_theme <- bs_theme(
    bg = "#fcfefe",
    fg = "#595959"
  )

  # ------------------------------------------------------------------------------

  theme_light_bl <- function(...) {
    ret <- ggplot2::theme_bw(...)

    col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)
    ret$panel.background <- col_rect
    ret$plot.background <- col_rect
    ret$legend.background <- col_rect
    ret$legend.key <- col_rect

    larger_x_text <- ggplot2::element_text(size = rel(1.25))
    larger_y_text <- ggplot2::element_text(size = rel(1.25), angle = 90)
    ret$axis.text.x <- larger_x_text
    ret$axis.text.y <- larger_y_text
    ret$axis.title.x <- larger_x_text
    ret$axis.title.y <- larger_y_text

    ret$legend.position <- "top"

    ret
  }

  col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)

  maybe_lm <- function(x) {
    try(lm(y ~ poly(x, input$piecewise_deg), data = x), silent = TRUE)
  }

  expansion_to_tibble <- function(x, original, prefix = "term ") {
    cls <- class(x)[1]
    nms <- recipes::names0(ncol(x), prefix)
    colnames(x) <- nms
    x <- as_tibble(x)
    x$variable <- original
    res <- tidyr::pivot_longer(x, cols = c(-variable))
    if (cls != "poly") {
      res <- res[res$value > .Machine$double.eps, ]
    }
    res
  }

  mult_poly <- function(dat, degree = 4) {
    rng <- extendrange(dat$x, f = .025)
    grid <- seq(rng[1], rng[2], length.out = 1000)
    grid_df <- tibble(x = grid)
    feat <- poly(grid_df$x, degree)
    res <- expansion_to_tibble(feat, grid_df$x)

    # make some random names so that we can plot the features with distinct colors
    rand_names <- lapply(1:degree, function(x) {
      paste0(sample(letters)[1:10], collapse = "")
    })
    rand_names <- unlist(rand_names)
    rand_names <- tibble(name = unique(res$name), name2 = rand_names)
    res <-
      dplyr::inner_join(res, rand_names, by = dplyr::join_by(name)) |>
      dplyr::select(-name) |>
      dplyr::rename(name = name2)
    res
  }

  # ------------------------------------------------------------------------------

  spline_example <- tibble(x = fossil$age, y = fossil$strontium.ratio)
  rng <- extendrange(fossil$age, f = .025)
  grid <- seq(rng[1], rng[2], length.out = 1000)
  grid_df <- tibble(x = grid)
  alphas <- 1 / 4
  line_wd <- 1.0

  base_p <-
    spline_example |>
    ggplot(aes(x = x, y = y)) +
    geom_point(alpha = 3 / 4, pch = 1, cex = 3) +
    labs(x = "Age", y = "Isotope Ratio") +
    lims(x = rng) +
    theme_light_bl(base_size = 16)

  output$global <- renderPlot({
    poly_fit <- lm(y ~ poly(x, input$global_deg), data = spline_example)
    poly_pred <-
      predict(poly_fit, grid_df, interval = "confidence", level = .90) |>
      bind_cols(grid_df)

    global_p <- base_p

    if (input$global_deg > 0) {
      global_p <-
        global_p +
        geom_ribbon(
          data = poly_pred,
          aes(y = NULL, ymin = lwr, ymax = upr),
          alpha = 1 / 8
        ) +
        geom_line(
          data = poly_pred,
          aes(y = fit),
          col = "black",
          linewidth = line_wd
        ) +
        theme(
          plot.margin = margin(t = -20, r = 0, b = 0, l = 0),
          panel.background = col_rect,
          plot.background = col_rect,
          legend.background = col_rect,
          legend.key = col_rect
        )

      feature_p <-
        poly(grid_df$x, input$global_deg) |>
        expansion_to_tibble(grid_df$x) |>
        ggplot(aes(variable, y = value, group = name, col = name)) +
        geom_line(show.legend = FALSE) + # , linewidth = 1, alpha = 1 / 2
        theme_void() +
        theme(
          plot.margin = margin(t = 0, r = 0, b = -20, l = 0),
          panel.background = col_rect,
          plot.background = col_rect,
          legend.background = col_rect,
          legend.key = col_rect
        ) +
        scale_color_viridis(discrete = TRUE, option = "turbo")

      p <- (feature_p / global_p) + plot_layout(heights = c(1.5, 4))
    }

    print(p)
  })
}

app <- shinyApp(ui = ui, server = server)

Issues with polynomial expansion

Variance is high as number of polynomial terms increases
Confidence intervals expand rapidly
Overfitting
Global pattern not always appropriate

Split polynomial fits to different regions

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| label: fig-piecewise-polynomials
#| viewerHeight: 700
#| viewerWidth: "100%"
#| standalone: true

library(shiny)
library(patchwork)
library(dplyr)
library(tidyr)
library(ggplot2)
library(splines2)
library(bslib)
library(viridis)
library(aspline)

data(fossil)

ui <- page_fillable(
  theme = bs_theme(
    bg = "#fcfefe",
    fg = "#595959",
    base_font = "Atkinson Hyperlegible",
    font_scale = 1.5
  ),
  padding = "1rem",
  tags$head(
    tags$style(
      type = 'text/css',
      '.irs-grid-text {font-size: 20px;}', # For grid values (min, max, ticks)
      '.irs-single {font-size: 24px;}' # For the currently selected value on the handle
    )
  ),
  layout_columns(
    fill = FALSE,
    col_widths = breakpoints(sm = c(-1, 5, 5, -1)),
    sliderInput(
      "piecewise_deg",
      label = "Polynomial Degree",
      min = 0L,
      max = 6L,
      step = 1L,
      value = 4L
    ), # sliderInput
    sliderInput(
      "cuts",
      label = "Cutpoints",
      min = 93L,
      max = 122L,
      step = 1,
      value = c(101, 118)
    ) # sliderInput
  ), # layout_columns
  layout_columns(
    fill = FALSE,
    col_widths = breakpoints(sm = c(-1, 10, -1)),
    as_fill_carrier(plotOutput('pieces', height = "500px"))
  )
)

server <- function(input, output, session) {
  light_bg <- "#fcfefe" # from aml4td.scss
  grid_theme <- bs_theme(
    bg = "#fcfefe",
    fg = "#595959"
  )

  # ------------------------------------------------------------------------------

  theme_light_bl <- function(...) {
    ret <- ggplot2::theme_bw(...)

    col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)
    ret$panel.background <- col_rect
    ret$plot.background <- col_rect
    ret$legend.background <- col_rect
    ret$legend.key <- col_rect

    larger_x_text <- ggplot2::element_text(size = rel(1.25))
    larger_y_text <- ggplot2::element_text(size = rel(1.25), angle = 90)
    ret$axis.text.x <- larger_x_text
    ret$axis.text.y <- larger_y_text
    ret$axis.title.x <- larger_x_text
    ret$axis.title.y <- larger_y_text

    ret$legend.position <- "top"

    ret
  }

  col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)

  maybe_lm <- function(x) {
    try(lm(y ~ poly(x, input$piecewise_deg), data = x), silent = TRUE)
  }

  expansion_to_tibble <- function(x, original, prefix = "term ") {
    cls <- class(x)[1]
    nms <- recipes::names0(ncol(x), prefix)
    colnames(x) <- nms
    x <- as_tibble(x)
    x$variable <- original
    res <- tidyr::pivot_longer(x, cols = c(-variable))
    if (cls != "poly") {
      res <- res[res$value > .Machine$double.eps, ]
    }
    res
  }

  mult_poly <- function(dat, degree = 4) {
    rng <- extendrange(dat$x, f = .025)
    grid <- seq(rng[1], rng[2], length.out = 1000)
    grid_df <- tibble(x = grid)
    feat <- poly(grid_df$x, degree)
    res <- expansion_to_tibble(feat, grid_df$x)

    # make some random names so that we can plot the features with distinct colors
    rand_names <- lapply(1:degree, function(x) {
      paste0(sample(letters)[1:10], collapse = "")
    })
    rand_names <- unlist(rand_names)
    rand_names <- tibble(name = unique(res$name), name2 = rand_names)
    res <-
      dplyr::inner_join(res, rand_names, by = dplyr::join_by(name)) |>
      dplyr::select(-name) |>
      dplyr::rename(name = name2)
    res
  }

  # ------------------------------------------------------------------------------

  spline_example <- tibble(x = fossil$age, y = fossil$strontium.ratio)
  rng <- extendrange(fossil$age, f = .025)
  grid <- seq(rng[1], rng[2], length.out = 1000)
  grid_df <- tibble(x = grid)
  alphas <- 1 / 4
  line_wd <- 1.0

  base_p <-
    spline_example |>
    ggplot(aes(x = x, y = y)) +
    geom_point(alpha = 3 / 4, pch = 1, cex = 3) +
    labs(x = "Age", y = "Isotope Ratio") +
    theme_light_bl(base_size = 16)

  output$pieces <- renderPlot({
    cuts <- c(0, sort(input$cuts), 60)
    piece_cols <- c("#1B9E77", "#D95F02", "#7570B3")
    piece_p <- base_p

    if (input$piecewise_deg > 0) {
      data_splt <-
        spline_example |>
        dplyr::mutate(x_cut = cut(x, breaks = cuts, include.lowest = TRUE)) |>
        tidyr::nest(.by = x_cut) |>
        mutate(
          fit = lapply(data, maybe_lm),
          features = lapply(data, mult_poly, degree = input$piecewise_deg)
        )
      grid_splt <-
        dplyr::tibble(x = grid) |>
        dplyr::mutate(x_cut = cut(x, breaks = cuts, include.lowest = TRUE)) |>
        tidyr::nest(.by = x_cut)

      for (i in 1:3) {
        sub_pred <- grid_splt$data[[i]]
        if (!inherits(data_splt$fit[[i]], "try-error")) {
          sub_pred <-
            sub_pred |>
            dplyr::bind_cols(predict(
              data_splt$fit[[i]],
              sub_pred,
              interval = "confidence",
              level = .90
            ))

          piece_p <-
            piece_p +
            geom_ribbon(
              data = sub_pred,
              aes(y = NULL, ymin = lwr, ymax = upr),
              alpha = 1 / 15
            ) +
            geom_line(
              data = sub_pred,
              aes(y = fit),
              linewidth = line_wd
            )
        }
      }

      set.seed(383) # to control colors
      feature_p <-
        data_splt |>
        dplyr::select(features) |>
        tidyr::unnest(features) |>
        ggplot(aes(x = variable, y = value, col = name)) +
        geom_line(show.legend = FALSE) +
        theme_void() +
        theme(
          plot.margin = margin(t = 0, r = 0, b = -20, l = 0),
          panel.background = col_rect,
          plot.background = col_rect,
          legend.background = col_rect,
          legend.key = col_rect
        ) +
        scale_color_viridis(discrete = TRUE, option = "turbo")

      p <- (feature_p / piece_p) + plot_layout(heights = c(1, 4))
    }

    print(p)
  })
}

app <- shinyApp(ui = ui, server = server)

Polynomial splines

Basis expansion creates different regions of the predictor space using boundaries called knots
Within each region, use polynomial functions
Ensure globally we have a smooth, continuous function

Simple spline functions

#| '!! shinylive warning !!': |
#|   shinylive does not work in self-contained HTML documents.
#|   Please set `embed-resources: false` in your metadata.
#| label: fig-simple-spline
#| viewerHeight: 700
#| viewerWidth: "100%"
#| standalone: true
library(shiny)
library(patchwork)
library(dplyr)
library(tidyr)
library(ggplot2)
library(bslib)
library(aspline)

data(fossil)

ui <- page_fillable(
  theme = bs_theme(
    bg = "#fcfefe",
    fg = "#595959",
    base_font = "Atkinson Hyperlegible",
    font_scale = 1.5
  ),
  padding = "1rem",
  tags$head(
    tags$style(
      type = 'text/css',
      '.irs-grid-text {font-size: 20px;}', # For grid values (min, max, ticks)
      '.irs-single {font-size: 24px;}' # For the currently selected value on the handle
    )
  ),
  layout_columns(
    fill = FALSE,
    col_widths = breakpoints(sm = c(-2, 8, -2)),
    sliderInput(
      "cuts",
      label = "Cutpoints",
      min = 93L,
      max = 122L,
      step = 1,
      value = c(107, 114)
    ) # sliderInput
  ), # layout_columns
  layout_columns(
    fill = FALSE,
    col_widths = breakpoints(sm = c(-1, 10, -1)),
    as_fill_carrier(plotOutput('splime_spline', height = "500px"))
  )
)

server <- function(input, output, session) {
  light_bg <- "#fcfefe" # from aml4td.scss
  grid_theme <- bs_theme(
    bg = "#fcfefe",
    fg = "#595959"
  )

  # ------------------------------------------------------------------------------

  theme_light_bl <- function(...) {
    ret <- ggplot2::theme_bw(...)

    col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)
    ret$panel.background <- col_rect
    ret$plot.background <- col_rect
    ret$legend.background <- col_rect
    ret$legend.key <- col_rect

    larger_x_text <- ggplot2::element_text(size = rel(1.25))
    larger_y_text <- ggplot2::element_text(size = rel(1.25), angle = 90)
    ret$axis.text.x <- larger_x_text
    ret$axis.text.y <- larger_y_text
    ret$axis.title.x <- larger_x_text
    ret$axis.title.y <- larger_y_text

    ret$legend.position <- "top"

    ret
  }

  col_rect <- ggplot2::element_rect(fill = light_bg, colour = light_bg)

  # ------------------------------------------------------------------------------

  spline_example <- tibble(x = fossil$age, y = fossil$strontium.ratio)
  rng <- extendrange(fossil$age, f = .025)
  grid <- seq(rng[1], rng[2], length.out = 1000)
  grid_df <- tibble(x = grid)
  alphas <- 1 / 4
  line_wd <- 1.0

  base_p <-
    spline_example |>
    ggplot(aes(x = x, y = y)) +
    geom_point(alpha = 3 / 4, pch = 1, cex = 3) +
    labs(x = "Age", y = "Isotope Ratio") +
    theme_light_bl(base_size = 16)

  output$splime_spline <- renderPlot({
    spline_p <- base_p

    h <- function(x) {
      ifelse(x > 0, x, 0)
    }

    mod_dat <-
      spline_example |>
      mutate(
        x_2 = x^2,
        x_3 = x^3,
        x_k_1 = pmax(h(x - min(input$cuts))^3, 0),
        x_k_2 = pmax(h(x - max(input$cuts))^3, 0)
      )

    grid_spln <-
      grid_df |>
      mutate(
        x_2 = x^2,
        x_3 = x^3,
        x_k_1 = pmax(h(x - min(input$cuts))^3, 0),
        x_k_2 = pmax(h(x - max(input$cuts))^3, 0)
      )

    features <-
      rbind(
        tibble::tibble(x = grid_spln$x, value = grid_spln$x_k_1, term = "4") |>
          filter(value != 0),
        tibble::tibble(x = grid_spln$x, value = grid_spln$x_k_2, term = "5") |>
          filter(value != 0)
      )

    fit_1 <- lm(y ~ ., data = mod_dat)
    spline_pred <-
      predict(fit_1, grid_spln, interval = "confidence", level = .90) |>
      bind_cols(grid_df)

    spline_p <-
      spline_p +
      geom_ribbon(
        data = spline_pred,
        aes(y = NULL, ymin = lwr, ymax = upr),
        alpha = 1 / 15
      ) +
      geom_line(
        data = spline_pred,
        aes(y = fit),
        linewidth = line_wd
      ) +
      geom_vline(
        xintercept = min(input$cuts),
        col = "#A6CEE3",
        lty = 2,
        linewidth = 1
      ) +
      geom_vline(
        xintercept = max(input$cuts),
        col = "#1F78B4",
        lty = 2,
        linewidth = 1
      )

    term_p <-
      features |>
      ggplot(aes(x, value, col = term)) +
      geom_line(show.legend = FALSE, linewidth = 1) +
      lims(x = rng) +
      theme_void() +
      theme(
        plot.margin = margin(t = 0, r = 0, b = -20, l = 0),
        panel.background = col_rect,
        plot.background = col_rect,
        legend.background = col_rect,
        legend.key = col_rect
      ) +
      scale_color_brewer(palette = "Paired")

    p <- (term_p / spline_p) + plot_layout(heights = c(1, 4))

    print(p)
  })
}

app <- shinyApp(ui = ui, server = server)

How to define the knots

$n$ groups with equal number of observations

How many knots? Tuning!

Wrap-up

Recap

Variables can be rescaled to reduce skewness, sometimes improving model performance
Basis expansions and splines can be used to model non-linear relationships
Always compare outcomes of different models to ensure transformations or nonlinear components improve model performance

Build better data (II)

Announcements

Announcements

Learning objectives

Problems with numeric predictors

Potential issues with numeric predictors

Skewed variables

Outliers

📝 What to do with outliers?

Options

1 : 1 transformations

Transformation functions

Transformation functions

Box-Cox procedure

Box-Cox procedure

Yeo-Johnson

How is \(\lambda\) determined?

Result of transformation

Standardizing to a common scale

Normalization

Standardizing to a common scale

Interactions

Interactive effects

Incorporating interactive effects

Interpreting interactive terms

When to include interaction terms?

📝 Identifying interactive effects

Non-linear features

Basis expansion

Polynomial expansion

Polynomial expansion

Issues with polynomial expansion

Split polynomial fits to different regions

Polynomial splines

Simple spline functions

How to define the knots

Wrap-up

Recap