Tuning hyperparameters

Lecture 7

Dr. Benjamin Soltoff

Cornell University
INFO 4940/5940 - Fall 2024

September 19, 2024

Announcements

No new homework this week

Learning objectives

Review tuning parameters for machine learning models
Define boosted trees models
Utilize grid search to optimize tuning parameters
Implement space-filling designs for grid searches
Introduce iterative search procedures for tuning parameters
Implement Bayesian optimization using the {tune} package
Finalize the model for production

Application exercise

`ae-06`

Go to the course GitHub org and find your ae-06 (repo name will be suffixed with your GitHub name).
Clone the repo in RStudio, open the Quarto document in the repo, install the required packages, and follow along and complete the exercises.
Render, commit, and push your edits by the AE deadline – end of the day

From last time

library(tidymodels)
library(textrecipes)
library(bonsai)

reg_metrics <- metric_set(mae, rsq)

data(hotel_rates)
set.seed(295)
hotel_rates <- hotel_rates |>
  sample_n(5000) |>
  arrange(arrival_date) |>
  select(-arrival_date) |>
  mutate(
    company = factor(as.character(company)),
    country = factor(as.character(country)),
    agent = factor(as.character(agent))
  )

Previously - Data Usage

set.seed(421)
hotel_split <- initial_split(hotel_rates, strata = avg_price_per_room)

hotel_train <- training(hotel_split)
hotel_test <- testing(hotel_split)

set.seed(531)
hotel_rs <- vfold_cv(hotel_train, strata = avg_price_per_room)

Previously - Feature engineering

library(textrecipes)

hash_rec <- recipe(avg_price_per_room ~ ., data = hotel_train) |>
  step_YeoJohnson(lead_time) |>
  # Defaults to 32 signed indicator columns
  step_dummy_hash(agent) |>
  step_dummy_hash(company) |>
  # Regular indicators for the others
  step_dummy(all_nominal_predictors()) |>
  step_zv(all_predictors())

Optimizing models via tuning parameters

Tuning parameters

Some model or preprocessing parameters cannot be estimated directly from the data.

Some examples:

✅ Tree depth in decision trees
✅ Number of neighbors in a K-nearest neighbor model
✅ Number of features to hash in a feature hashing recipe
❌ Bayesian priors for model parameters
❌ The random seed

Optimize tuning parameters

Try different values and measure their performance.
Find good values for these parameters.
Once the value(s) of the parameter(s) are determined, a model can be finalized by fitting the model to the entire training set.

Tagging parameters for tuning

With {tidymodels}, you can mark the parameters that you want to optimize with a value of tune().

The function itself just returns… itself:

tune()

tune()

str(tune())

 language tune()

# optionally add a label
tune("my hash")

tune("my hash")

Optimizing the hash features

Our new recipe is:

hash_rec <- recipe(avg_price_per_room ~ ., data = hotel_train) |>
  step_YeoJohnson(lead_time) |>
  step_dummy_hash(agent, num_terms = tune("agent hash")) |>
  step_dummy_hash(company, num_terms = tune("company hash")) |>
  step_zv(all_predictors())

We will be using a tree-based model in a minute.

The other categorical predictors are left as-is.
That’s why there is no step_dummy().

Boosting models

Boosting

Bagging - use bootstrap resampling to create multiple copies of training data, fit a separate model to each copy, and aggregate the results
Grow trees independently
Boosting - grow trees sequentially

How do you study?

Slow, methodical preparation

Cram the night before

Which is more effective in the long run? Learning slowly

Boosted trees

Fit a decision tree to the residuals from the model
Add the tree to the model and update the residuals
Repeat steps 1 and 2 until complete

Each tree is small - only a handful of terminal nodes

Each tree uses the results of the previous tree to better predict samples, especially those that have been poorly predicted.

Each tree in the ensemble is saved and new samples are predicted using a weighted average of the votes of each tree in the ensemble.

Popular implementations

Adaboost (Adaptive Boosting)
Gradient boosting
LightGBM (Light Gradient Boosting Machine)
XGBoost (Extreme Gradient Boosting)

Boosted tree tuning parameters

Some possible parameters:

mtry: The number of predictors randomly sampled at each split (in \([1, ncol(x)]\) or \((0, 1]\)).
trees: The number of trees (\([1, \infty]\), but usually up to thousands)
min_n: The number of samples needed to further split (\([1, n]\)).
learn_rate: The rate that each tree adapts from previous iterations (\((0, \infty]\), usual maximum is 0.1).
stop_iter: The number of iterations of boosting where no improvement was shown before stopping (\([1, trees]\))

Boosted tree tuning parameters

It is usually not difficult to optimize these models.

Often, there are multiple candidate tuning parameter combinations that have very good results.

To demonstrate simple concepts, we’ll look at optimizing the number of trees in the ensemble (between 1 and 100) and the learning rate (\(10^{-5}\) to \(10^{-1}\)).

Boosted tree tuning parameters

We’ll need to load the {bonsai} package. This has the information needed to use LightGBM

library(bonsai)
lgbm_spec <- boost_tree(trees = tune(), learn_rate = tune()) |>
  set_mode("regression") |>
  set_engine("lightgbm")

lgbm_wflow <- workflow(hash_rec, lgbm_spec)

Optimize tuning parameters

The main two strategies for optimization are:

Grid search 💠 which tests a pre-defined set of candidate values
Iterative search 🌀 which suggests/estimates new values of candidate parameters to evaluate

Grid search

A small grid of points trying to minimize the error via learning rate:

Grid search

In reality we would probably sample the space more densely:

Iterative Search

We could start with a few points and search the space:

Grid search

Parameters

The {tidymodels} framework provides pre-defined information on tuning parameters (such as their type, range, transformations, etc).
The extract_parameter_set_dials() function extracts these tuning parameters and the info.

Grids

Create your grid manually or automatically.
The grid_*() functions can make a grid.

Different types of grids

Space-filling designs (SFD) attempt to cover the parameter space without redundant candidates.

Create a grid

lgbm_wflow |>
  extract_parameter_set_dials()

Collection of 4 parameters for tuning

   identifier       type    object
        trees      trees nparam[+]
   learn_rate learn_rate nparam[+]
   agent hash  num_terms nparam[+]
 company hash  num_terms nparam[+]

# Individual functions:
trees()

# Trees (quantitative)
Range: [1, 2000]

learn_rate()

Learning Rate (quantitative)
Transformer: log-10 [1e-100, Inf]
Range (transformed scale): [-10, -1]

A parameter set can be updated (e.g. to change the ranges).

Create a grid

set.seed(12)
grid <- lgbm_wflow |>
  extract_parameter_set_dials() |>
  grid_space_filling(size = 25)

grid

# A tibble: 25 × 4
   trees learn_rate `agent hash` `company hash`
   <int>      <dbl>        <int>          <int>
 1     1   7.50e- 6          574            574
 2    84   1.78e- 5         2048           2298
 3   167   5.62e-10         1824            912
 4   250   4.22e- 5         3250            512
 5   334   1.78e- 8          512           2896
 6   417   1.33e- 3          322           1625
 7   500   1   e- 1         1448           1149
 8   584   1   e- 7         1290            256
 9   667   2.37e-10          456            724
10   750   1.78e- 2          645            322
# ℹ 15 more rows

⏱️ Your turn

Create a grid for our tunable workflow.

Try creating a regular grid.

03:00

Create a regular grid

set.seed(12)
grid <- lgbm_wflow |>
  extract_parameter_set_dials() |>
  grid_regular(levels = 4)

grid

# A tibble: 256 × 4
   trees   learn_rate `agent hash` `company hash`
   <int>        <dbl>        <int>          <int>
 1     1 0.0000000001          256            256
 2   667 0.0000000001          256            256
 3  1333 0.0000000001          256            256
 4  2000 0.0000000001          256            256
 5     1 0.0000001             256            256
 6   667 0.0000001             256            256
 7  1333 0.0000001             256            256
 8  2000 0.0000001             256            256
 9     1 0.0001                256            256
10   667 0.0001                256            256
# ℹ 246 more rows

⏱️ Your turn

What advantage would a regular grid have?

01:00

Update parameter ranges

lgbm_param <- lgbm_wflow |>
  extract_parameter_set_dials() |>
  update(
    trees = trees(c(1L, 100L)),
    learn_rate = learn_rate(c(-5, -1))
  )

set.seed(712)
grid <- lgbm_param |>
  grid_regular(size = 25)

grid

# A tibble: 81 × 4
   trees learn_rate `agent hash` `company hash`
   <int>      <dbl>        <int>          <int>
 1     1    0.00001          256            256
 2    50    0.00001          256            256
 3   100    0.00001          256            256
 4     1    0.001            256            256
 5    50    0.001            256            256
 6   100    0.001            256            256
 7     1    0.1              256            256
 8    50    0.1              256            256
 9   100    0.1              256            256
10     1    0.00001         1024            256
# ℹ 71 more rows

The results

grid |>
  ggplot(aes(trees, learn_rate)) +
  geom_point(size = 4) +
  scale_y_log10()

Note that the learning rates are uniform on the log-10 scale and this shows 2 of 4 dimensions.

Use the `tune_*()` functions to tune models

Choosing tuning parameters

Let’s take our previous model and tune more parameters:

lgbm_spec <- boost_tree(trees = tune(), learn_rate = tune(), min_n = tune()) |>
  set_mode("regression") |>
  set_engine("lightgbm")

lgbm_wflow <- workflow(hash_rec, lgbm_spec)

# Update the feature hash ranges (log-2 units)
lgbm_param <- lgbm_wflow |>
  extract_parameter_set_dials() |>
  update(
    `agent hash` = num_hash(c(3, 8)),
    `company hash` = num_hash(c(3, 8))
  )

Grid search

set.seed(9)
ctrl <- control_grid(save_pred = TRUE)

lgbm_res <- lgbm_wflow |>
  tune_grid(
    resamples = hotel_rs,
    grid = 25,
    # The options below are not required by default
    param_info = lgbm_param,
    control = ctrl,
    metrics = reg_metrics
  )

Grid search

lgbm_res

# Tuning results
# 10-fold cross-validation using stratification 
# A tibble: 10 × 5
   splits             id     .metrics          .notes           .predictions
   <list>             <chr>  <list>            <list>           <list>      
 1 <split [3372/377]> Fold01 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 2 <split [3373/376]> Fold02 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 3 <split [3373/376]> Fold03 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 4 <split [3373/376]> Fold04 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 5 <split [3373/376]> Fold05 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 6 <split [3374/375]> Fold06 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 7 <split [3375/374]> Fold07 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 8 <split [3376/373]> Fold08 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
 9 <split [3376/373]> Fold09 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>    
10 <split [3376/373]> Fold10 <tibble [50 × 9]> <tibble [0 × 3]> <tibble>

Grid results

autoplot(lgbm_res)

Tuning results

collect_metrics(lgbm_res)

# A tibble: 50 × 11
   trees min_n learn_rate `agent hash` `company hash` .metric .estimator   mean
   <int> <int>      <dbl>        <int>          <int> <chr>   <chr>       <dbl>
 1   298    19   4.15e- 9          222             36 mae     standard   53.5  
 2   298    19   4.15e- 9          222             36 rsq     standard    0.816
 3  1394     5   5.82e- 6           28             21 mae     standard   53.2  
 4  1394     5   5.82e- 6           28             21 rsq     standard    0.817
 5   774    12   4.41e- 2           27             95 mae     standard    9.86 
 6   774    12   4.41e- 2           27             95 rsq     standard    0.949
 7  1342     7   6.84e-10           71             17 mae     standard   53.5  
 8  1342     7   6.84e-10           71             17 rsq     standard    0.816
 9   669    39   8.62e- 7          141            145 mae     standard   53.5  
10   669    39   8.62e- 7          141            145 rsq     standard    0.817
# ℹ 40 more rows
# ℹ 3 more variables: n <int>, std_err <dbl>, .config <chr>

Tuning results

collect_metrics(lgbm_res, summarize = FALSE)

# A tibble: 500 × 10
   id     trees min_n  learn_rate `agent hash` `company hash` .metric .estimator
   <chr>  <int> <int>       <dbl>        <int>          <int> <chr>   <chr>     
 1 Fold01   298    19     4.15e-9          222             36 mae     standard  
 2 Fold01   298    19     4.15e-9          222             36 rsq     standard  
 3 Fold02   298    19     4.15e-9          222             36 mae     standard  
 4 Fold02   298    19     4.15e-9          222             36 rsq     standard  
 5 Fold03   298    19     4.15e-9          222             36 mae     standard  
 6 Fold03   298    19     4.15e-9          222             36 rsq     standard  
 7 Fold04   298    19     4.15e-9          222             36 mae     standard  
 8 Fold04   298    19     4.15e-9          222             36 rsq     standard  
 9 Fold05   298    19     4.15e-9          222             36 mae     standard  
10 Fold05   298    19     4.15e-9          222             36 rsq     standard  
# ℹ 490 more rows
# ℹ 2 more variables: .estimate <dbl>, .config <chr>

Choose a parameter combination

show_best(lgbm_res, metric = "rsq")

# A tibble: 5 × 11
  trees min_n learn_rate `agent hash` `company hash` .metric .estimator  mean
  <int> <int>      <dbl>        <int>          <int> <chr>   <chr>      <dbl>
1  1890    10    0.0159           115            174 rsq     standard   0.950
2   774    12    0.0441            27             95 rsq     standard   0.949
3  1638    36    0.0409            15            120 rsq     standard   0.948
4   963    23    0.00556          157             13 rsq     standard   0.937
5   590     5    0.00320           85             73 rsq     standard   0.911
# ℹ 3 more variables: n <int>, std_err <dbl>, .config <chr>

Choose a parameter combination

Create your own tibble for final parameters or use one of the tune::select_*() functions:

lgbm_best <- select_best(lgbm_res, metric = "mae")
lgbm_best

# A tibble: 1 × 6
  trees min_n learn_rate `agent hash` `company hash` .config              
  <int> <int>      <dbl>        <int>          <int> <chr>                
1  1890    10     0.0159          115            174 Preprocessor12_Model1

Checking calibration

library(probably)
lgbm_res |>
  collect_predictions(
    parameters = lgbm_best
  ) |>
  cal_plot_regression(
    truth = avg_price_per_room,
    estimate = .pred
  )

Running in parallel

Grid search, combined with resampling, requires fitting a lot of models!
These models don’t depend on one another and can be run in parallel.

We can use a parallel backend to do this:

library(future)

# use all available cores
plan(multisession, workers = availableCores())

# on RStudio Workbench, be demure
# and share the cores!
plan(multisession, workers = 4)

# Now call `tune_grid()`!

Running in parallel

Speed-ups are fairly linear up to the number of physical cores (10 here).

Early stopping for boosted trees

We have directly optimized the number of trees as a tuning parameter.

Instead we could

Set the number of trees to a single large number.
Stop adding trees when performance gets worse.

This is known as “early stopping” and there is a parameter for that: stop_iter.

Early stopping has a potential to decrease the tuning time.

⏱️ Your turn

Set trees = 2000 and tune the stop_iter parameter.

Note that you will need to regenerate lgbm_param with your new workflow!

10:00

lgbm_spec <- boost_tree(trees = 2000, learn_rate = tune(),
                        min_n = tune(), stop_iter = tune()) |>
  set_mode("regression") |>
  set_engine("lightgbm")

lgbm_wflow <- workflow(hash_rec, lgbm_spec)

# Update the feature hash ranges (log-2 units)
lgbm_param <- lgbm_wflow |>
  extract_parameter_set_dials() |>
  update(
    `agent hash` = num_hash(c(3, 8)),
    `company hash` = num_hash(c(3, 8))
  )

# tune the model
lgbm_res <- lgbm_wflow |>
  tune_grid(
    resamples = hotel_rs,
    grid = 25,
    # The options below are not required by default
    param_info = lgbm_param,
    control = ctrl,
    metrics = reg_metrics
  )

autoplot(lgbm_res)

show_best(lgbm_res, metric = "mae")

# A tibble: 5 × 11
  min_n learn_rate stop_iter `agent hash` `company hash` .metric .estimator
  <int>      <dbl>     <int>        <int>          <int> <chr>   <chr>     
1     9    0.0712         12           61             28 mae     standard  
2    12    0.0180          6           13              9 mae     standard  
3    30    0.0409         13           37             44 mae     standard  
4    24    0.00495         4           92             28 mae     standard  
5    33    0.00200        14           23             11 mae     standard  
# ℹ 4 more variables: mean <dbl>, n <int>, std_err <dbl>, .config <chr>

Our boosting model

We used feature hashing to generate a smaller set of indicator columns to deal with the large number of levels for the agent and country predictors.

Tree-based models (and a few others) don’t require indicators for categorical predictors. They can split on these variables as-is.

We’ll keep all categorical predictors as factors and focus on optimizing additional boosting parameters.

Our Boosting Model

lgbm_spec <- boost_tree(
  trees = 1000, learn_rate = tune(), min_n = tune(),
  tree_depth = tune(), loss_reduction = tune(),
  stop_iter = tune()
) |>
  set_mode("regression") |>
  set_engine("lightgbm")

lgbm_wflow <- workflow(avg_price_per_room ~ ., lgbm_spec)

lgbm_param <- lgbm_wflow |>
  extract_parameter_set_dials() |>
  update(learn_rate = learn_rate(c(-5, -1)))

Iterative search

Instead of pre-defining a grid of candidate points, we can model our current results to predict what the next candidate point should be.

Suppose that we are only tuning the learning rate in our boosted tree.

We could do something like:

mae_pred <- lm(mae ~ learn_rate, data = resample_results)

and use this to predict and rank new learning rate candidates.

Iterative Search

A linear model probably isn’t the best choice though (more in a minute).

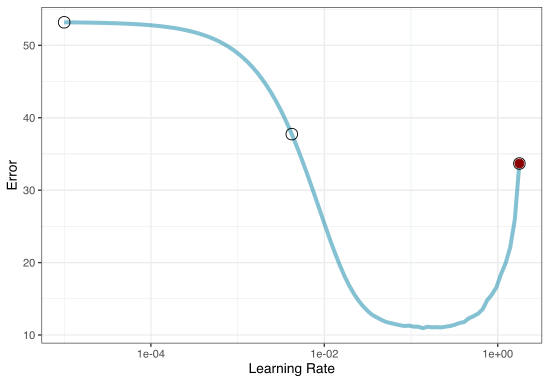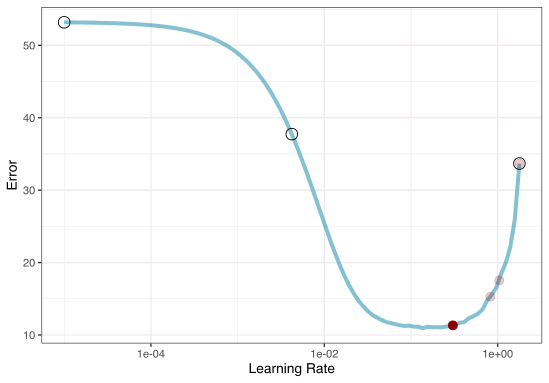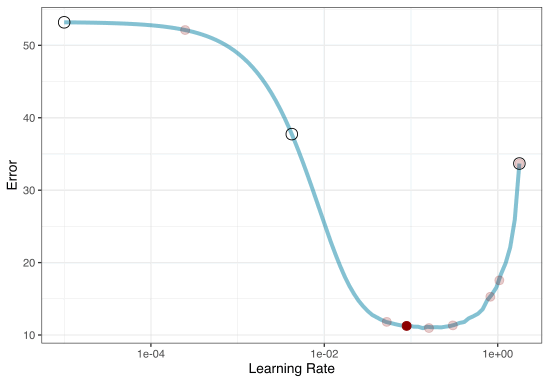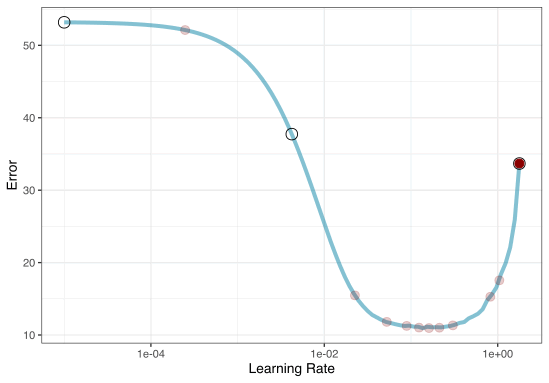
To illustrate the process, we resampled a large grid of learning rate values for our data to show what the relationship is between MAE and learning rate.

Now suppose that we used a grid of three points in the parameter range for learning rate…

A large grid

A three point grid

Bayesian optimization

A sequential method that uses a model to predict new candidate parameters for assessment
When scoring potential parameter value, the mean and variance of performance are predicted
The strategy used to define how these two statistical quantities are used is defined by an acquisition function

Acquisition function

Acquisition functions take the predicted mean and variance and use them to balance:

exploration: new candidates should explore new areas.
exploitation: new candidates must stay near existing values.

Exploration focuses on the variance, exploitation is about the mean.

Acquisition functions

We’ll use an acquisition function to select a new candidate.

The most popular method appears to be expected improvement (EI) above the current best results.

Zero at existing data points.
The expected improvement is integrated over all possible improvement (“expected” in the probability sense).

We would probably pick the point with the largest EI as the next point.

(There are other functions beyond EI.)

Iteration

Once we pick the candidate point, we measure performance for it (e.g. resampling).

Another GP is fit, EI is recomputed, and so on.

We stop when we have completed the allowed number of iterations or if we don’t see any improvement after a pre-set number of attempts.

GP evolution

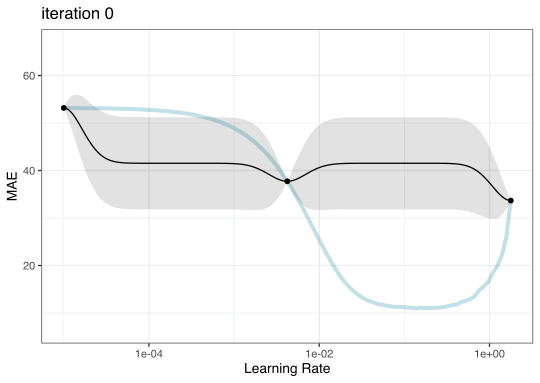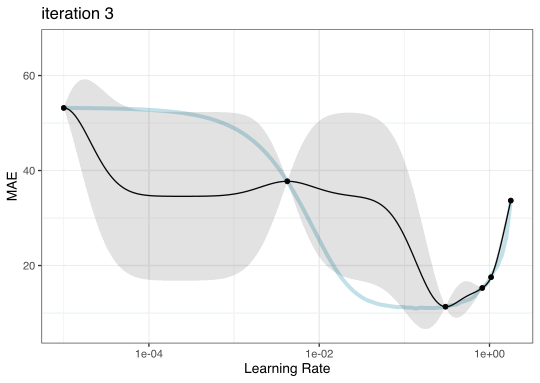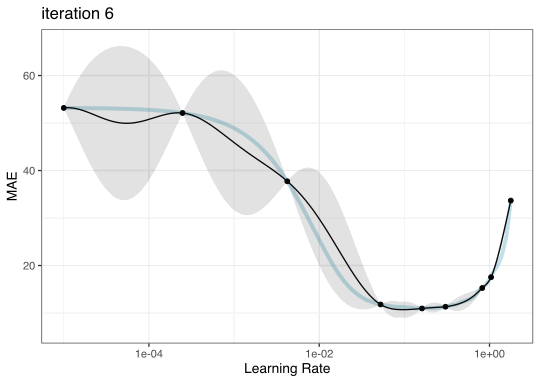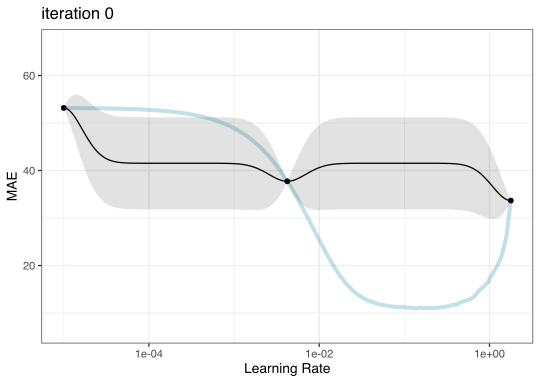
BO in {tidymodels}

We’ll use a function called tune_bayes() that has very similar syntax to tune_grid().

It has an additional initial argument for the initial set of performance estimates and parameter combinations for the GP model.

Initial grid points

initial can be the results of another tune_*() function or an integer (in which case tune_grid() is used under to hood to make such an initial set of results).

We’ll run the optimization more than once, so let’s make an initial grid of results to serve as the substrate for the BO.

An initial grid

reg_metrics <- metric_set(mae, rsq)

set.seed(12)
init_res <- lgbm_wflow |>
  tune_grid(
    resamples = hotel_rs,
    grid = nrow(lgbm_param) + 2,
    param_info = lgbm_param,
    metrics = reg_metrics
  )

show_best(init_res, metric = "mae") |> select(-.metric, -.estimator)

# A tibble: 5 × 9
  min_n tree_depth learn_rate loss_reduction stop_iter  mean     n std_err
  <int>      <int>      <dbl>          <dbl>     <int> <dbl> <int>   <dbl>
1     9          4   0.0415         5.21e- 9        13  9.96    10   0.176
2    16         12   0.0136         1.91e- 3         9 10.1     10   0.156
3    25          8   0.00256        9.58e-10         7 14.2     10   0.174
4    22          9   0.00154        5.77e- 6         5 19.2     10   0.170
5    32          3   0.000144       3.02e+ 1        18 47.9     10   0.302
# ℹ 1 more variable: .config <chr>

BO using {tidymodels}

ctrl_bo <- control_bayes(verbose_iter = TRUE) # <- for demonstration

set.seed(15)
lgbm_bayes_res <- lgbm_wflow |>
  tune_bayes(
    resamples = hotel_rs,
    initial = init_res, # <- initial results
    iter = 20,
    param_info = lgbm_param,
    control = ctrl_bo,
    metrics = reg_metrics
  )

Optimizing mae using the expected improvement

── Iteration 1 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.964 (@iter 0)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=32, tree_depth=12, learn_rate=0.0178, loss_reduction=1.03e-10,
  stop_iter=12

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=10.02 (+/-0.155)

── Iteration 2 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.964 (@iter 0)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=15, tree_depth=14, learn_rate=0.0977, loss_reduction=0.00535,
  stop_iter=4

i Estimating performance

✓ Estimating performance

♥ Newest results:   mae=9.707 (+/-0.167)

── Iteration 3 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.707 (@iter 2)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=15, tree_depth=2, learn_rate=0.0986, loss_reduction=2.65,
  stop_iter=20

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=10.86 (+/-0.177)

── Iteration 4 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.707 (@iter 2)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=12, tree_depth=12, learn_rate=0.0308, loss_reduction=2.16e-06,
  stop_iter=3

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.801 (+/-0.142)

── Iteration 5 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.707 (@iter 2)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=37, tree_depth=15, learn_rate=0.0501, loss_reduction=1.89,
  stop_iter=9

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.807 (+/-0.155)

── Iteration 6 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.707 (@iter 2)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=9, tree_depth=14, learn_rate=0.0624, loss_reduction=0.000108,
  stop_iter=3

i Estimating performance

✓ Estimating performance

♥ Newest results:   mae=9.567 (+/-0.145)

── Iteration 7 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.567 (@iter 6)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=11, tree_depth=2, learn_rate=0.0441, loss_reduction=0.0203,
  stop_iter=3

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=11.46 (+/-0.203)

── Iteration 8 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.567 (@iter 6)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=13, tree_depth=15, learn_rate=0.0385, loss_reduction=2.86e-09,
  stop_iter=18

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.64 (+/-0.139)

── Iteration 9 ─────────────────────────────────────────────────────────────────

i Current best:     mae=9.567 (@iter 6)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=8, tree_depth=8, learn_rate=0.064, loss_reduction=1.22e-06,
  stop_iter=20

i Estimating performance

✓ Estimating performance

♥ Newest results:   mae=9.55 (+/-0.151)

── Iteration 10 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=39, tree_depth=7, learn_rate=0.0888, loss_reduction=1.36e-10,
  stop_iter=9

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.855 (+/-0.157)

── Iteration 11 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=17, tree_depth=13, learn_rate=0.0683, loss_reduction=3.25e-10,
  stop_iter=11

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.65 (+/-0.161)

── Iteration 12 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=6, tree_depth=6, learn_rate=0.0102, loss_reduction=9.86e-10,
  stop_iter=19

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=10.4 (+/-0.189)

── Iteration 13 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=4, tree_depth=11, learn_rate=0.0414, loss_reduction=0.00021,
  stop_iter=15

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.567 (+/-0.16)

── Iteration 14 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=19, tree_depth=14, learn_rate=0.00693, loss_reduction=0.0704,
  stop_iter=19

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=10.63 (+/-0.185)

── Iteration 15 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=2, tree_depth=11, learn_rate=0.0701, loss_reduction=7.25e-06,
  stop_iter=19

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.581 (+/-0.15)

── Iteration 16 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=2, tree_depth=6, learn_rate=0.0631, loss_reduction=26.7, stop_iter=17

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=10.16 (+/-0.171)

── Iteration 17 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.55 (@iter 9)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=4, tree_depth=13, learn_rate=0.0524, loss_reduction=9.64e-09,
  stop_iter=13

i Estimating performance

✓ Estimating performance

♥ Newest results:   mae=9.547 (+/-0.173)

── Iteration 18 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.547 (@iter 17)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=16, tree_depth=12, learn_rate=0.04, loss_reduction=6.77e-07,
  stop_iter=17

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=9.611 (+/-0.149)

── Iteration 19 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.547 (@iter 17)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=17, tree_depth=15, learn_rate=0.0107, loss_reduction=1.33e-09,
  stop_iter=3

i Estimating performance

✓ Estimating performance

ⓧ Newest results:   mae=10.24 (+/-0.155)

── Iteration 20 ────────────────────────────────────────────────────────────────

i Current best:     mae=9.547 (@iter 17)

i Gaussian process model

✓ Gaussian process model

i Generating 5000 candidates

i Predicted candidates

i min_n=4, tree_depth=10, learn_rate=0.0592, loss_reduction=1.99e-10,
  stop_iter=11

i Estimating performance

✓ Estimating performance

♥ Newest results:   mae=9.493 (+/-0.161)

Best results

show_best(lgbm_bayes_res, metric = "mae") |> select(-.metric, -.estimator)

# A tibble: 5 × 10
  min_n tree_depth learn_rate loss_reduction stop_iter  mean     n std_err
  <int>      <int>      <dbl>          <dbl>     <int> <dbl> <int>   <dbl>
1     4         10     0.0592       1.99e-10        11  9.49    10   0.161
2     4         13     0.0524       9.64e- 9        13  9.55    10   0.173
3     8          8     0.0640       1.22e- 6        20  9.55    10   0.151
4     4         11     0.0414       2.10e- 4        15  9.57    10   0.160
5     9         14     0.0624       1.08e- 4         3  9.57    10   0.145
# ℹ 2 more variables: .config <chr>, .iter <int>

Plotting BO results

autoplot(lgbm_bayes_res, metric = "mae")

Plotting BO results

autoplot(lgbm_bayes_res, metric = "mae", type = "parameters")

Plotting BO results

autoplot(lgbm_bayes_res, metric = "mae", type = "performance")

ENHANCE

autoplot(lgbm_bayes_res, metric = "mae", type = "performance") +
  ylim(c(9, 14))

Notes

Stopping tune_bayes() will return the current results.
Parallel processing can still be used to more efficiently measure each candidate point.
There are a lot of other iterative methods that you can use.
The {finetune} package also has functions for simulated annealing search.

Finalizing the model

Let’s say that we’ve tried a lot of different models and we like our LightGBM model the most.

What do we do now?

Finalize the workflow by choosing the values for the tuning parameters.
Fit the model on the entire training set.
Verify performance using the test set.
Document and publish the model (later this semester)

Locking down the tuning parameters

We can take the results of the Bayesian optimization and accept the best results:

best_param <- select_best(lgbm_bayes_res, metric = "mae")
final_wflow <- lgbm_wflow |>
  finalize_workflow(best_param)
final_wflow

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Formula
Model: boost_tree()

── Preprocessor ────────────────────────────────────────────────────────────────
avg_price_per_room ~ .

── Model ───────────────────────────────────────────────────────────────────────
Boosted Tree Model Specification (regression)

Main Arguments:
  trees = 1000
  min_n = 4
  tree_depth = 10
  learn_rate = 0.0592446327108508
  loss_reduction = 1.9888406080826e-10
  stop_iter = 11

Computational engine: lightgbm

The final fit

We can use individual functions:

final_fit <- final_wflow |> fit(data = hotel_train)

# then predict() or augment() 
# then compute metrics

Remember that there is also a convenience function to do all of this:

set.seed(3893)
final_res <- final_wflow |> last_fit(hotel_split, metrics = reg_metrics)
final_res

# Resampling results
# Manual resampling 
# A tibble: 1 × 6
  splits              id               .metrics .notes   .predictions .workflow 
  <list>              <chr>            <list>   <list>   <list>       <list>    
1 <split [3749/1251]> train/test split <tibble> <tibble> <tibble>     <workflow>

Test set results

final_res |>
  collect_predictions() |>
  cal_plot_regression(
    truth = avg_price_per_room,
    estimate = .pred
  )

Test set performance:

final_res |> collect_metrics()

# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 mae     standard       9.73  Preprocessor1_Model1
2 rsq     standard       0.943 Preprocessor1_Model1

Recall that resampling predicted the MAE to be 9.49.

Wrap-up

Recap

Tuning parameters significantly impact the performance of models
Tuning parameters can be defined in both the feature engineering and model specification stages
Grid search is a simple but effective method for tuning parameters
Iterative search methods can be used to optimize parameters
Bayesian optimization is a sequential method that uses a model to predict new candidate parameters for assessment
The {tidymodels} framework provides functions for grid search and Bayesian optimization

Acknowledgments

Materials derived in part from Machine learning with {tidymodels} and licensed under a Creative Commons Attribution-ShareAlike 4.0 International (CC BY-SA) License.

Tuning hyperparameters

Announcements

Announcements

Learning objectives

Application exercise

ae-06

From last time

Previously - Data Usage

Previously - Feature engineering

Optimizing models via tuning parameters

Tuning parameters

Optimize tuning parameters

Tagging parameters for tuning

Optimizing the hash features

Boosting models

Boosting

How do you study?

Slow, methodical preparation

Cram the night before

Boosted trees

Popular implementations

Boosted tree tuning parameters

Boosted tree tuning parameters

Boosted tree tuning parameters

Optimize tuning parameters

Grid search

Grid search

Iterative Search

Grid search

Parameters

Grids

Different types of grids

Create a grid

Create a grid

⏱️ Your turn

Create a regular grid

⏱️ Your turn

Update parameter ranges

The results

Use the tune_*() functions to tune models

Choosing tuning parameters

Grid search

Grid search

Grid results

Tuning results

Tuning results

Choose a parameter combination

Choose a parameter combination

Checking calibration

Running in parallel

Running in parallel

Early stopping for boosted trees

⏱️ Your turn

Our boosting model

Our Boosting Model

Iterative search

Iterative Search

A large grid

A three point grid

Bayesian optimization

Acquisition function

Acquisition functions

Iteration

GP evolution

BO in {tidymodels}

Initial grid points

An initial grid

BO using {tidymodels}

Best results

Plotting BO results

Plotting BO results

Plotting BO results

ENHANCE

Notes

Finalizing the model

Finalizing the model

Locking down the tuning parameters

The final fit

Test set results

Wrap-up

`ae-06`

Use the `tune_*()` functions to tune models