Evaluate models using appropriate metrics

Lecture 8

Dr. Benjamin Soltoff

Cornell University
INFO 4940/5940 - Fall 2025

September 18, 2025

Announcements

Announcements

• Homework 03
• Project 1 coming soon

Learning objectives

• Define metrics for evaluating the performance of classification and regression models
• Identify trade-offs between different metrics
• Interpret different metrics
• Select appropriate metrics for a given modeling task

Data on forests in Washington

Data on forests in Washington

• The U.S. Forest Service maintains ML models to predict whether a plot of land is “forested.”
• This classification is important for all sorts of research, legislation, and land management purposes.
• Plots are typically remeasured every 10 years and this dataset contains the most recent measurement per plot.

Data on forests in Washington

• N = 7,107 plots of land, one from each of 7,107 6000-acre hexagons in WA.
• A nominal outcome, forested, with levels "Yes" and "No", measured “on-the-ground.”
• 18 remotely-sensed and easily-accessible predictors:
  • numeric variables based on weather and topography.
  • nominal variables based on classifications from other governmental orgs.

• Those nominal variables are classifications similar to “forested” but from other agencies. e.g. land_type is from the European Space Agency, and is a remotely-sensed 3-class distribution based on predictions for how the land is used.

Data on forests in Washington

# A tibble: 7,107 × 20
   forested  year elevation eastness northness roughness tree_no_tree dew_temp precip_annual
   <fct>    <dbl>     <dbl>    <dbl>     <dbl>     <dbl> <fct>           <dbl>         <dbl>
 1 Yes       2005       881       90        43        63 Tree             0.04           466
 2 Yes       2005       113      -25        96        30 Tree             6.4           1710
 3 No        2005       164      -84        53        13 Tree             6.06          1297
 4 Yes       2005       299       93        34         6 No tree          4.43          2545
 5 Yes       2005       806       47       -88        35 Tree             1.06           609
 6 Yes       2005       736      -27       -96        53 Tree             1.35           539
 7 Yes       2005       636      -48        87         3 No tree          1.42           702
 8 Yes       2005       224      -65       -75         9 Tree             6.39          1195
 9 Yes       2005        52      -62        78        42 Tree             6.5           1312
10 Yes       2005      2240      -67       -74        99 No tree         -5.63          1036
# ℹ 7,097 more rows
# ℹ 11 more variables: temp_annual_mean <dbl>, temp_annual_min <dbl>, temp_annual_max <dbl>,
#   temp_january_min <dbl>, vapor_min <dbl>, vapor_max <dbl>, canopy_cover <dbl>, lon <dbl>,
#   lat <dbl>, land_type <fct>, county <fct>

Partition and fit a very basic model

library(tidymodels)
library(forested)

set.seed(123)
forested_split <- initial_split(forested, prop = 0.8)
forested_train <- training(forested_split)
forested_test <- testing(forested_split)

tree_spec <- decision_tree(cost_complexity = 0.0001, mode = "classification")
forested_wflow <- workflow(forested ~ ., tree_spec)
forested_fit <- fit(forested_wflow, forested_train)

Looking at predictions

Looking at predictions

augment(forested_fit, new_data = forested_test)

# A tibble: 1,422 × 23
   .pred_class .pred_Yes .pred_No forested  year elevation eastness northness roughness tree_no_tree
   <fct>           <dbl>    <dbl> <fct>    <dbl>     <dbl>    <dbl>     <dbl>     <dbl> <fct>       
 1 Yes             0.977   0.0226 No        2005       164      -84        53        13 Tree        
 2 Yes             0.833   0.167  Yes       2005       299       93        34         6 No tree     
 3 No              0.154   0.846  Yes       2005       636      -48        87         3 No tree     
 4 No              0.25    0.75   Yes       2005       224      -65       -75         9 Tree        
 5 No              0.263   0.737  Yes       2005      2240      -67       -74        99 No tree     
 6 Yes             0.977   0.0226 Yes       2004      1044       96       -26        51 Tree        
 7 Yes             0.977   0.0226 Yes       2003      1031      -49        86       190 Tree        
 8 Yes             0.977   0.0226 Yes       2005      1330       99         7       212 Tree        
 9 Yes             0.977   0.0226 Yes       2005      1423       46        88       180 Tree        
10 Yes             0.977   0.0226 Yes       2014       546      -92       -38        28 Tree        
# ℹ 1,412 more rows
# ℹ 13 more variables: dew_temp <dbl>, precip_annual <dbl>, temp_annual_mean <dbl>,
#   temp_annual_min <dbl>, temp_annual_max <dbl>, temp_january_min <dbl>, vapor_min <dbl>,
#   vapor_max <dbl>, canopy_cover <dbl>, lon <dbl>, lat <dbl>, land_type <fct>, county <fct>

Confusion matrix

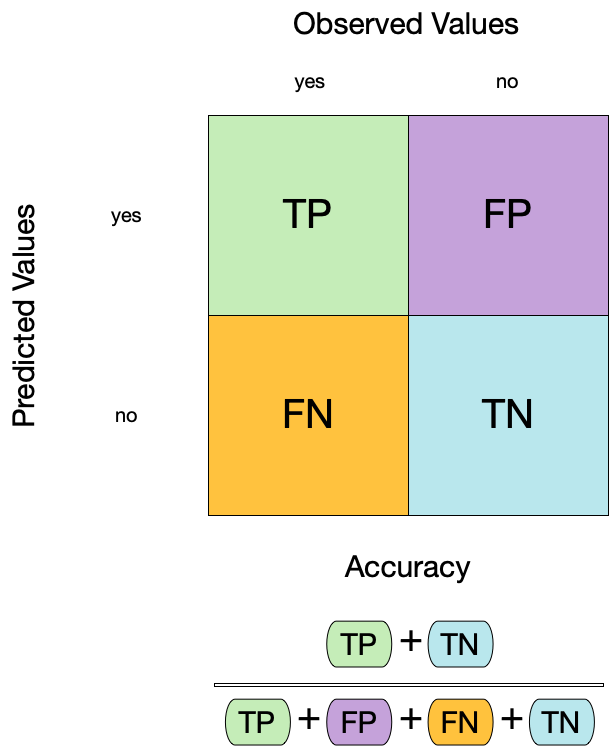
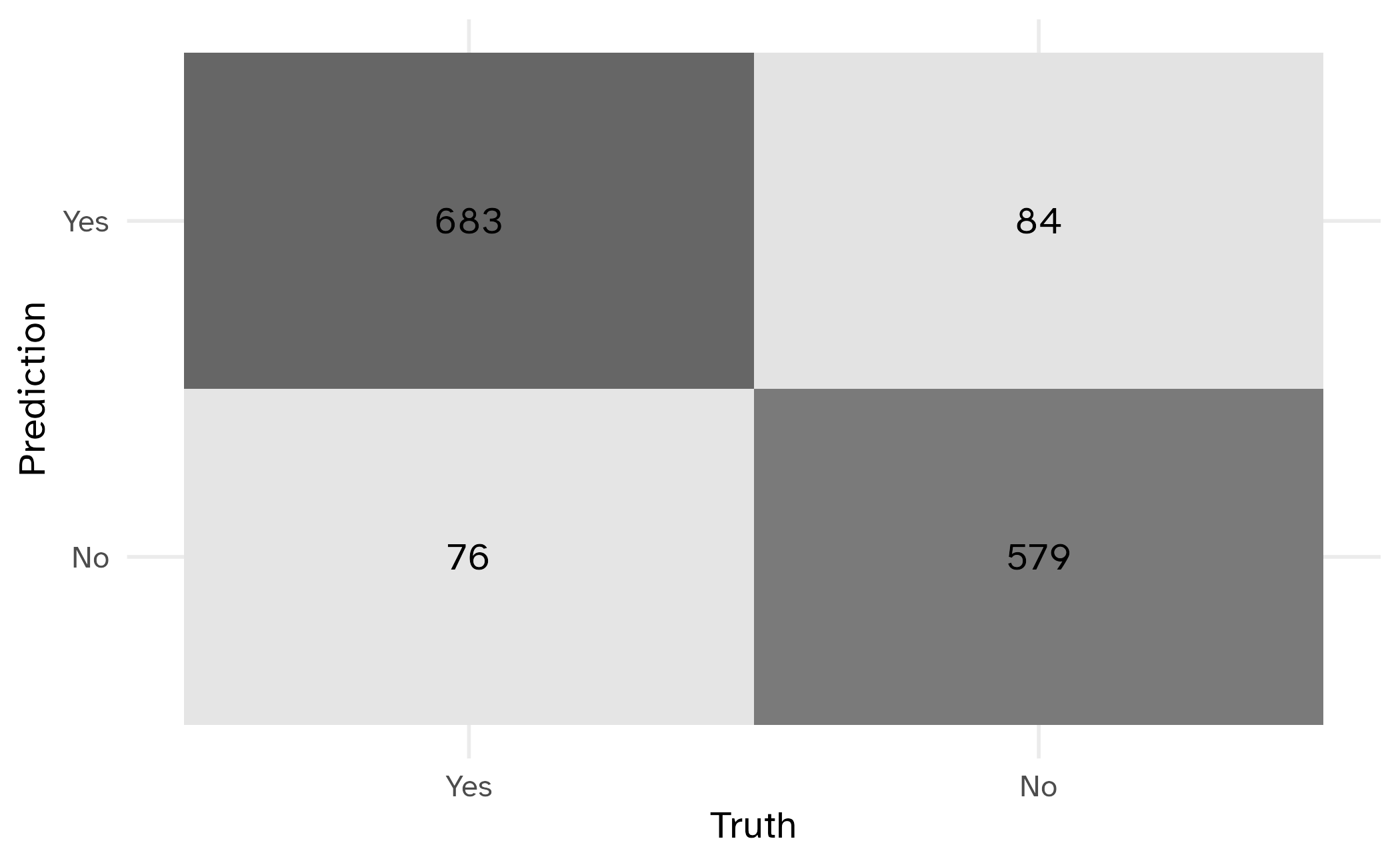
Confusion matrix

augment(forested_fit, new_data = forested_test) |>
  conf_mat(truth = forested, estimate = .pred_class)

          Truth
Prediction Yes  No
       Yes 683  84
       No   76 579

Confusion matrix

augment(forested_fit, new_data = forested_test) |>
  conf_mat(truth = forested, estimate = .pred_class) |>
  autoplot(type = "heatmap")

Metrics for model performance

Metrics for model performance

augment(forested_fit, new_data = forested_test) |>
  accuracy(truth = forested, estimate = .pred_class)

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy binary         0.887

The proportion of correctly predicted outcomes

There used to be a slide here calling out the pitfalls of accuracy when classes are imbalanced.

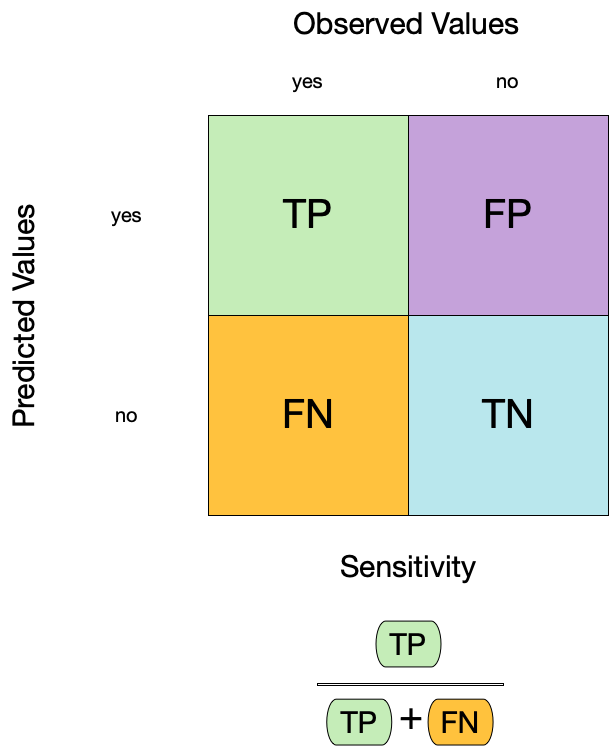
Sensitivity (TPR)

augment(forested_fit, new_data = forested_test) |>
  sensitivity(truth = forested, estimate = .pred_class)

# A tibble: 1 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 sensitivity binary         0.900

Proportion of correctly predicted events of interest

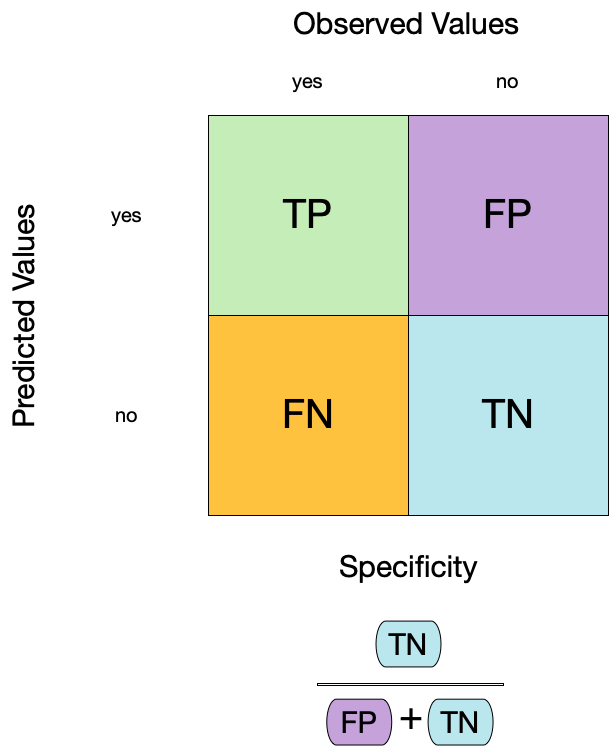
Specificity (TNR)

augment(forested_fit, new_data = forested_test) |>
  specificity(truth = forested, estimate = .pred_class)

# A tibble: 1 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 specificity binary         0.873

Proportion of correctly predicted non-events of interest

Metrics for model performance

forested_metrics <- metric_set(accuracy, specificity, sensitivity)

augment(forested_fit, new_data = forested_test) |>
  forested_metrics(truth = forested, estimate = .pred_class)

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary         0.887
2 specificity binary         0.873
3 sensitivity binary         0.900

Group differences in metrics

augment(forested_fit, new_data = forested_test) |>
  group_by(tree_no_tree) |>
  accuracy(truth = forested, estimate = .pred_class)

# A tibble: 2 × 4
  tree_no_tree .metric  .estimator .estimate
  <fct>        <chr>    <chr>          <dbl>
1 Tree         accuracy binary         0.899
2 No tree      accuracy binary         0.876

📝 Group differences in metrics

Instructions

Do any metrics differ substantially between groups? What does this mean?

# A tibble: 6 × 4
  tree_no_tree .metric     .estimator .estimate
  <fct>        <chr>       <chr>          <dbl>
1 Tree         accuracy    binary         0.899
2 No tree      accuracy    binary         0.876
3 Tree         specificity binary         0.372
4 No tree      specificity binary         0.940
5 Tree         sensitivity binary         0.964
6 No tree      sensitivity binary         0.583

03:00

The specificity for "Tree" is a good bit lower than it is for "No tree".

Specificity is the proportion of negatives that are correctly identified as negatives. “Negative” is the non-event level of the outcome, i.e. “non-forested.” So, when this index classifies the plot as having a tree, the model does not do well at correctly identifying the plot as non-forested when it is indeed non-forested.

Combined metrics

\(J\) index (combines sensitivity and specificity)

\[ J = \text{Sensitivity} + \text{Specificity} - 1 \]

\(F\)-score (combines precision and recall)

\[ F_{1}=2\left(\frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\right) \]

Two class data

These metrics assume that we know the threshold for converting “soft” probability predictions into “hard” class predictions.

Is a 50% threshold good?

What happens if we say that we need to be 80% sure to declare an event?

• sensitivity ⬇️, specificity ⬆️

What happens for a 20% threshold?

• sensitivity ⬆️, specificity ⬇️

Varying the threshold

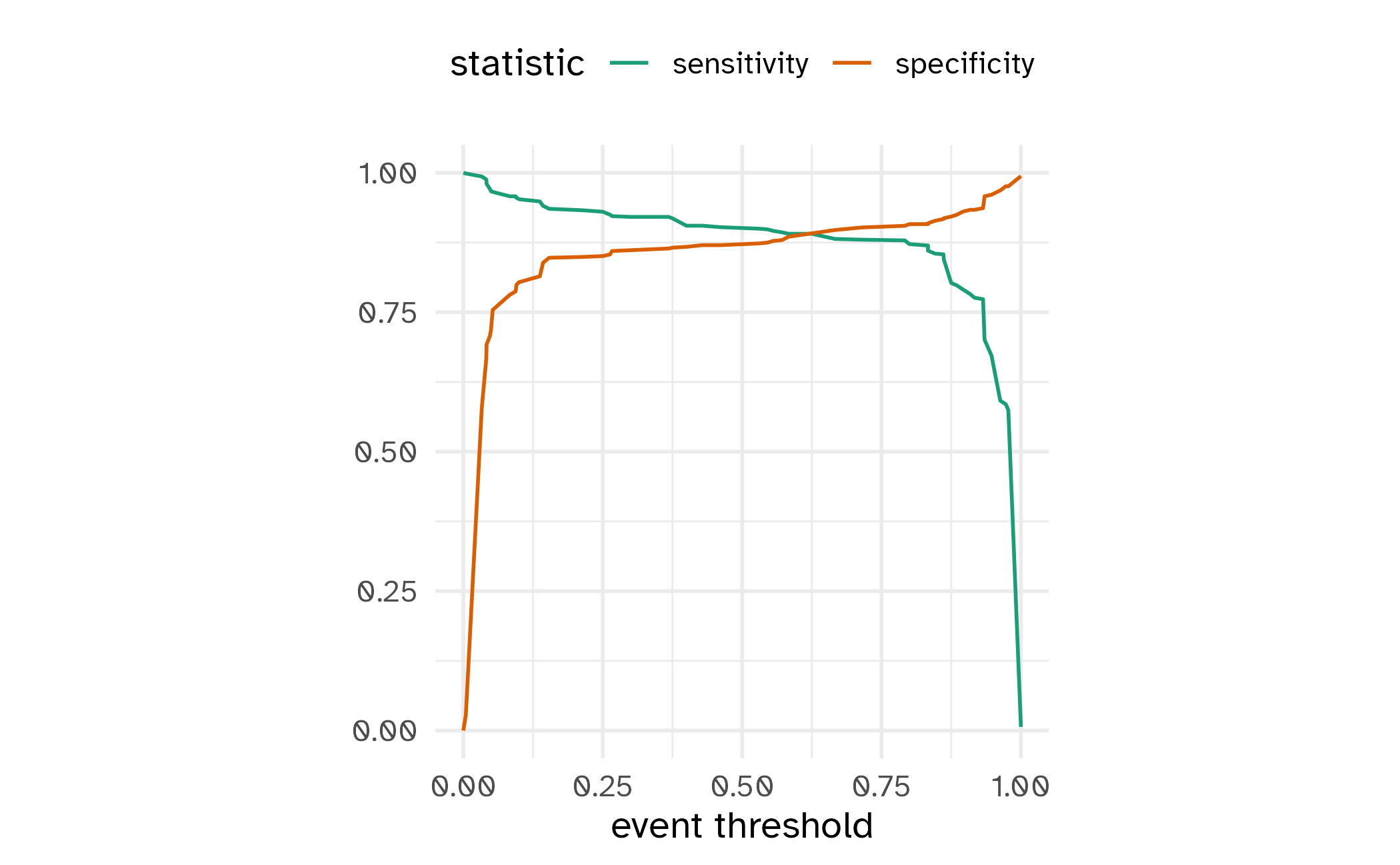
ROC curves

For an ROC (receiver operator characteristic) curve, we plot

• the false positive rate (1 - specificity) on the x-axis
• the true positive rate (sensitivity) on the y-axis

with sensitivity and specificity calculated at all possible thresholds.

ROC curves are insensitive to class imbalance.

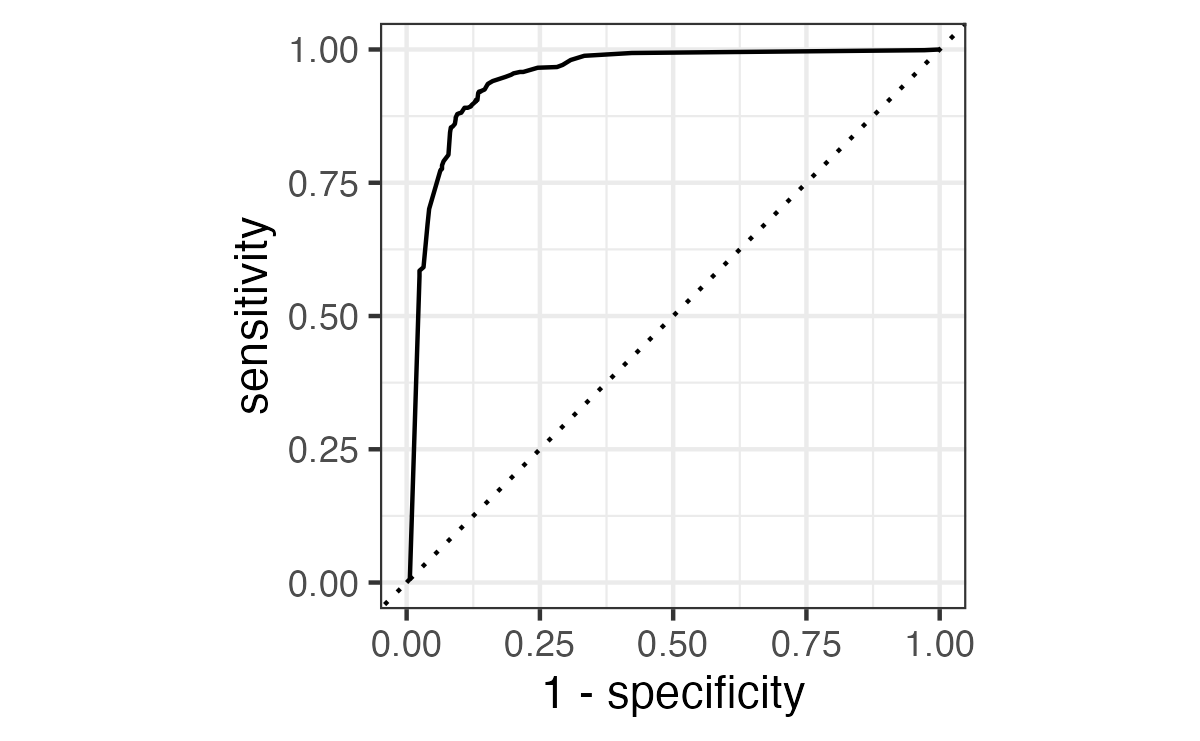
ROC curves

We can use the area under the ROC curve as a classification metric:

• ROC AUC = 1 💯
• ROC AUC = 1/2 😢

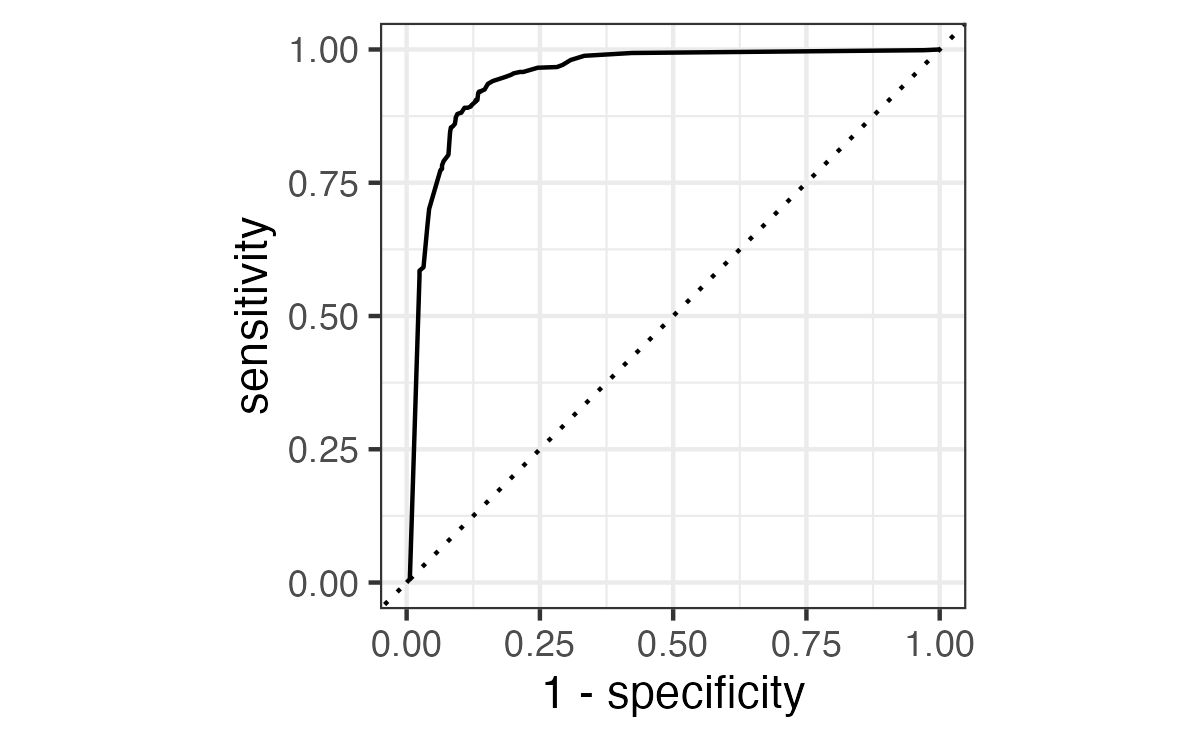
ROC curves

# ROC curve plot
augment(forested_fit, new_data = forested_test) |>
  roc_curve(
    truth = forested,
    .pred_Yes
  ) |>
  autoplot()
# ROC AUC value
augment(forested_fit, new_data = forested_test) |>
  roc_auc(truth = forested, .pred_Yes)

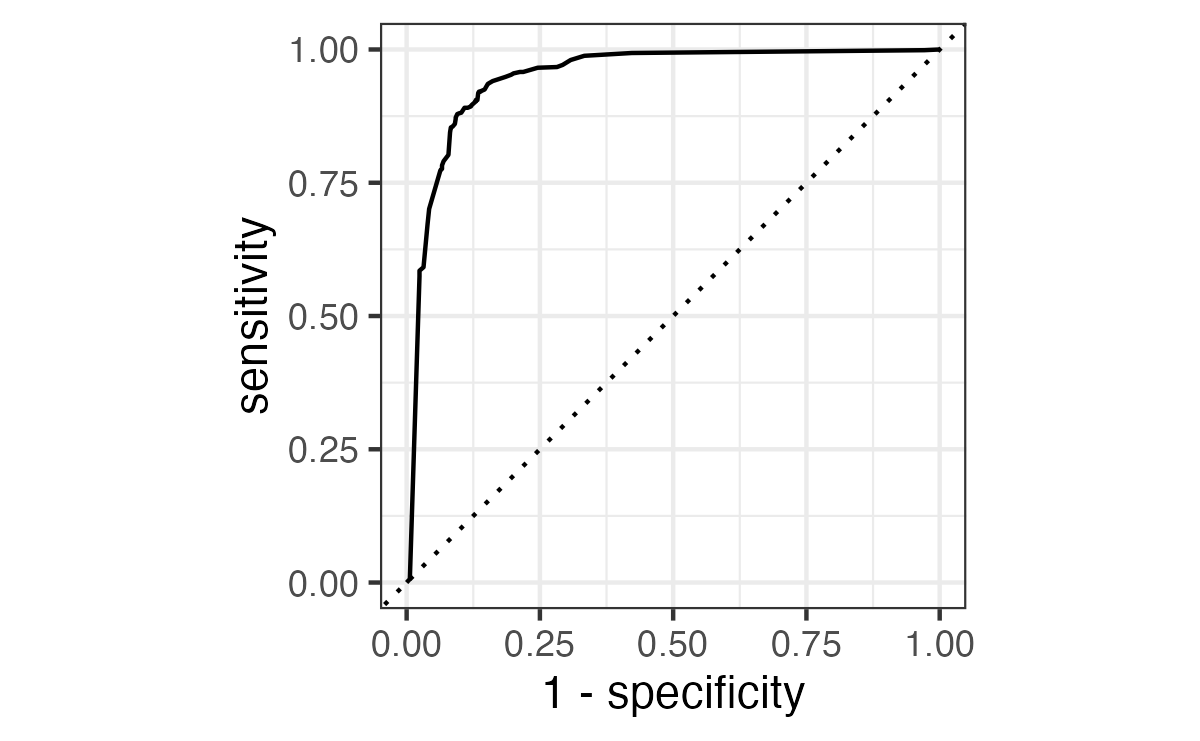
# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.948

Brier score

What if we don’t turn predicted probabilities into class predictions?

The Brier score is analogous to the mean squared error in regression models:

\[ \text{Brier}_{\text{class}} = \frac{1}{N}\sum_{i=1}^N\sum_{k=1}^C (y_{ik} - \hat{p}_{ik})^2 \]

Brier score

augment(forested_fit, new_data = forested_test) |>
  brier_class(truth = forested, .pred_Yes)

# A tibble: 1 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
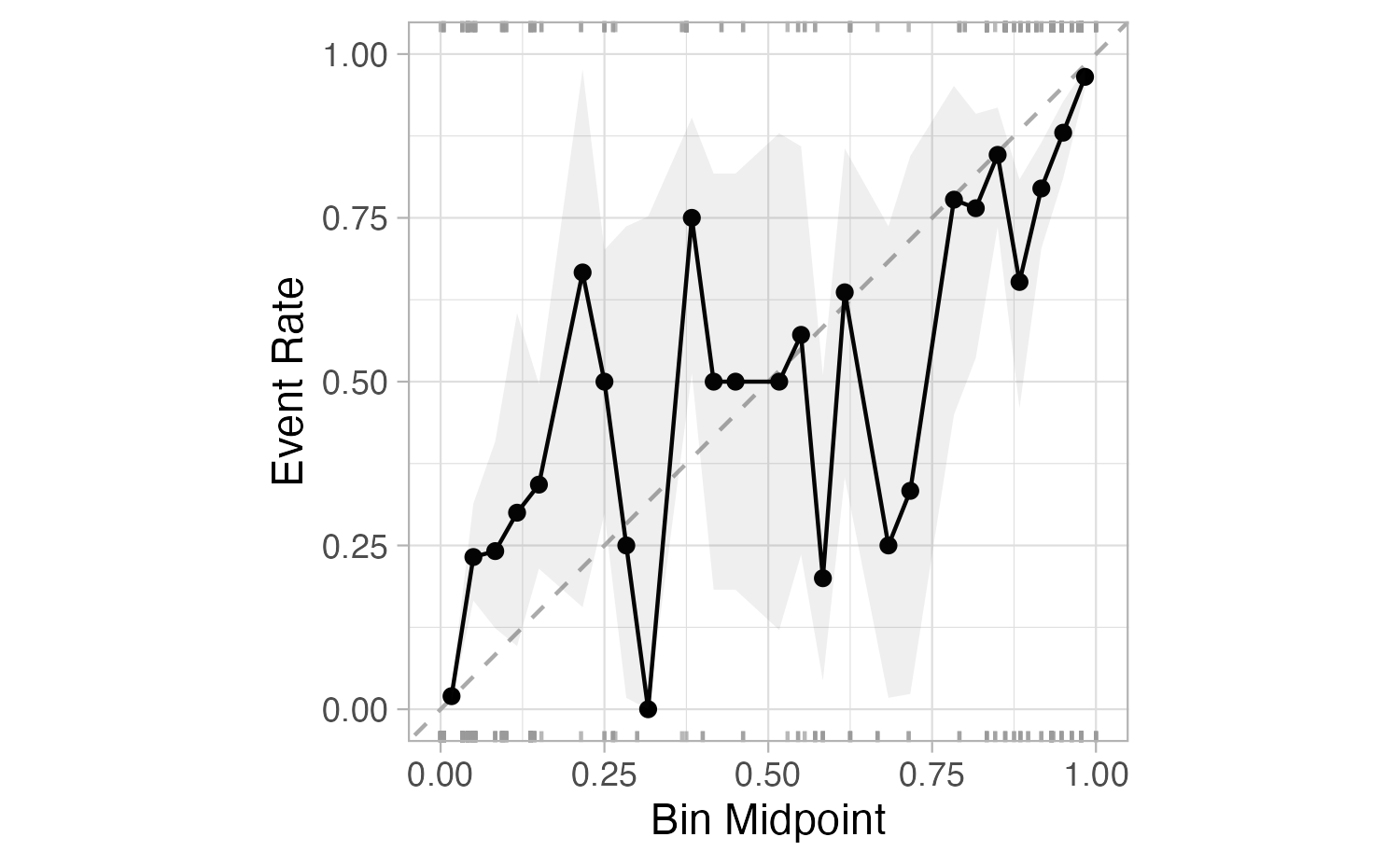
1 brier_class binary        0.0877

Smaller values are better, for binary classification the “bad model threshold” is about 0.25.

Separation vs calibration

The ROC captures separation

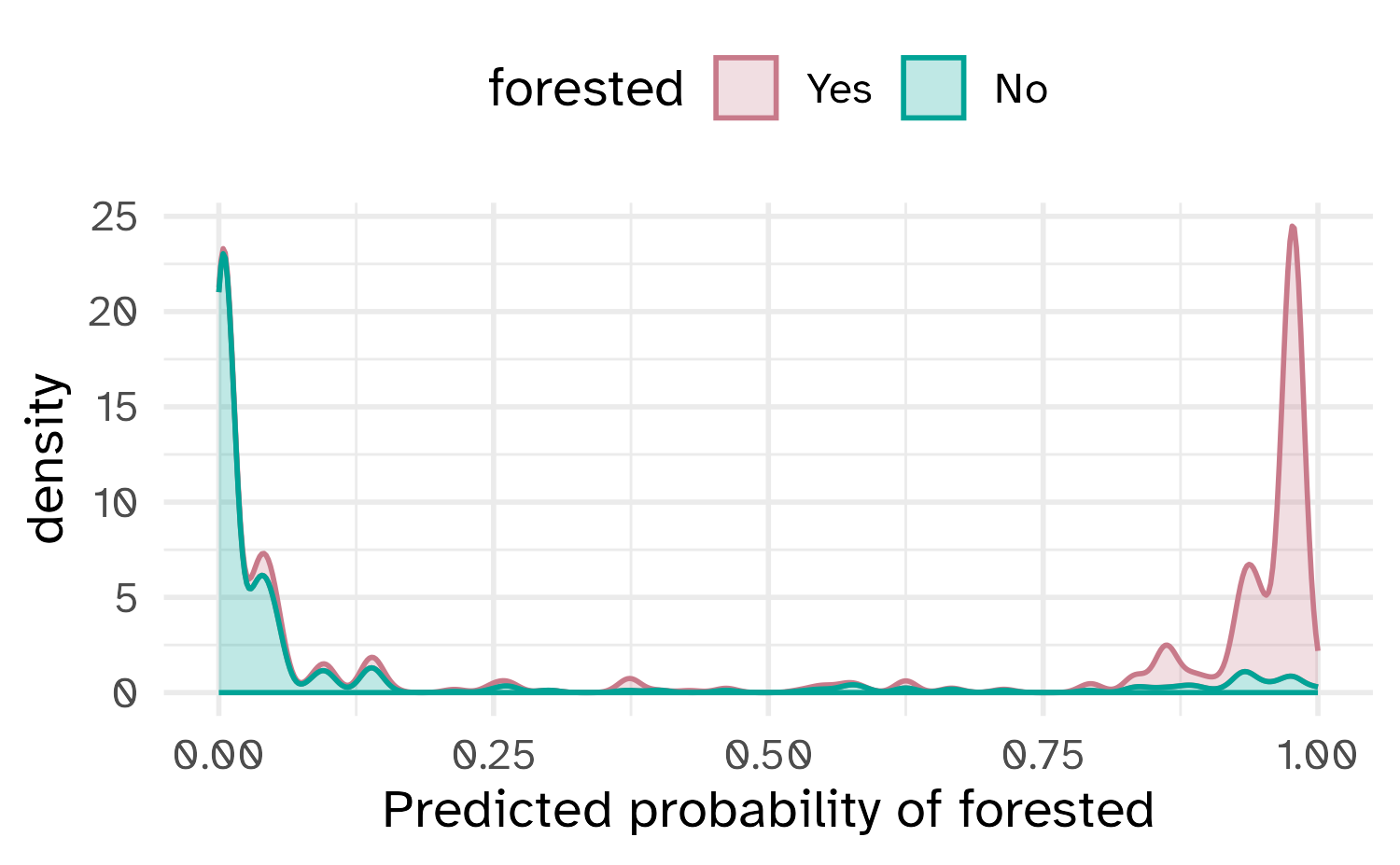
The Brier score captures calibration

• Good separation: the densities don’t overlap.
• Good calibration: the calibration line follows the diagonal.

Calibration plot: We bin observations according to predicted probability. In the bin for 20%-30% predicted prob, we should see an event rate of ~25% if the model is well-calibrated.

Common metrics for regression outcomes

Absolute error metrics

Expressed in the same units as the outcome of interest

Root mean squared error (RMSE)

\[ \text{RMSE} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2} \]

Mean absolute error (MAE)

\[ \text{MAE} = \frac{1}{n}\sum_{i=1}^{n}|y_i - \hat{y}_i| \]

RMSE is more sensitive to large errors than MAE

Percentage/relative error metrics

Expressed in relative terms, e.g. as a percentage of the actual value

Mean percentage error

\[ \text{MPE} = 100 \times \frac{1}{n}\sum_{i=1}^{n}\frac{y_i - \hat{y}_i}{y_i} \]

Mean absolute percent error

\[ \text{MAPE} = 100 \times \frac{1}{n}\sum_{i=1}^{n}\left|\frac{y_i - \hat{y}_i}{y_i}\right| \]

Equivalent to absolute error metrics, expressed in relative terms

Correlation metrics

Measure of correlation/consistency between predicted and actual values

R-squared

\[ R^2 = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}{\sum_{i=1}^{n}(y_i - \bar{y})^2} \]

Ranges from 0 to 1, higher values are better

Concordance correlation coefficient

\[ \rho_c = \frac{2\rho\sigma_y\sigma_\hat{y}}{\sigma_y^2 + \sigma_\hat{y}^2 + (\mu_y - \mu_\hat{y})^2} \]

Evaluates both the accuracy and consistency of predictions

Selecting appropriate metrics

Selecting appropriate metrics

1. Understand the type of problem

   • Classification (binary or multiclass)
   • Regression
   • Survival analysis
   • Clustering

2. Define objectives and prioritize errors

   • What stakeholders care about
   • Consequences of different types of errors

3. Consider data characteristics

   • Class imbalance
   • Outliers
   • Data distribution

4. Use multiple metrics (where possible)

   • Use a combined metric (e.g. \(F\)-score, \(J\)-index)
   • Desirability functions with {desirability2}

📝 Selecting appropriate metrics

Instructions

You’re evaluating a diagnostic model for COVID-19 detection based on symptoms (fever, cough, loss of taste/smell, fatigue, etc.) and rapid saliva testing.

• True Positive: Model correctly identifies COVID → Patient isolates, gets treatment, contact tracing begins

• False Positive: Model incorrectly flags healthy person as COVID → Unnecessary isolation, anxiety, lost work

• True Negative: Model correctly identifies non-COVID illness → Patient gets appropriate care, no isolation

• False Negative: Model misses COVID case → Patient spreads virus, no isolation, delayed treatment

Stakeholder	Most Important Metric	Least Acceptable Error Type	Why?
Individual Patient
Hospital administrator
Public Health Official
Workplace/School

10:00

1. Which stakeholders have conflicting priorities?

2. If you could only optimize for ONE metric, which would you choose and why?

3. How would your metric choice change during different phases of the pandemic (early outbreak vs. endemic phase)?

Wrap-up

Recap

• Metrics are used to evaluate model performance
• Different metrics capture different aspects of performance
• Select metrics that align with your goals and stakeholders

Acknowledgments

• Materials derived in part from Machine learning with {tidymodels} and licensed under a Creative Commons Attribution-ShareAlike 4.0 International (CC BY-SA) License.