Dimension reduction

Lecture 11

Dr. Benjamin Soltoff

Cornell University
INFO 4940/5940 - Fall 2024

October 3, 2024

Announcements

Homework 02
Complete team project preference survey in Canvas

Learning objectives

Distinguish unsupervised learning from supervised learning
Define dimension reduction and motivations for its usage
Introduce principal component analysis (PCA)
Define uniform manifold approximation and projection (UMAP)
Implement PCA and UMAP using {recipes}
Interpret the results of PCA and UMAP

What is unsupervised learning?

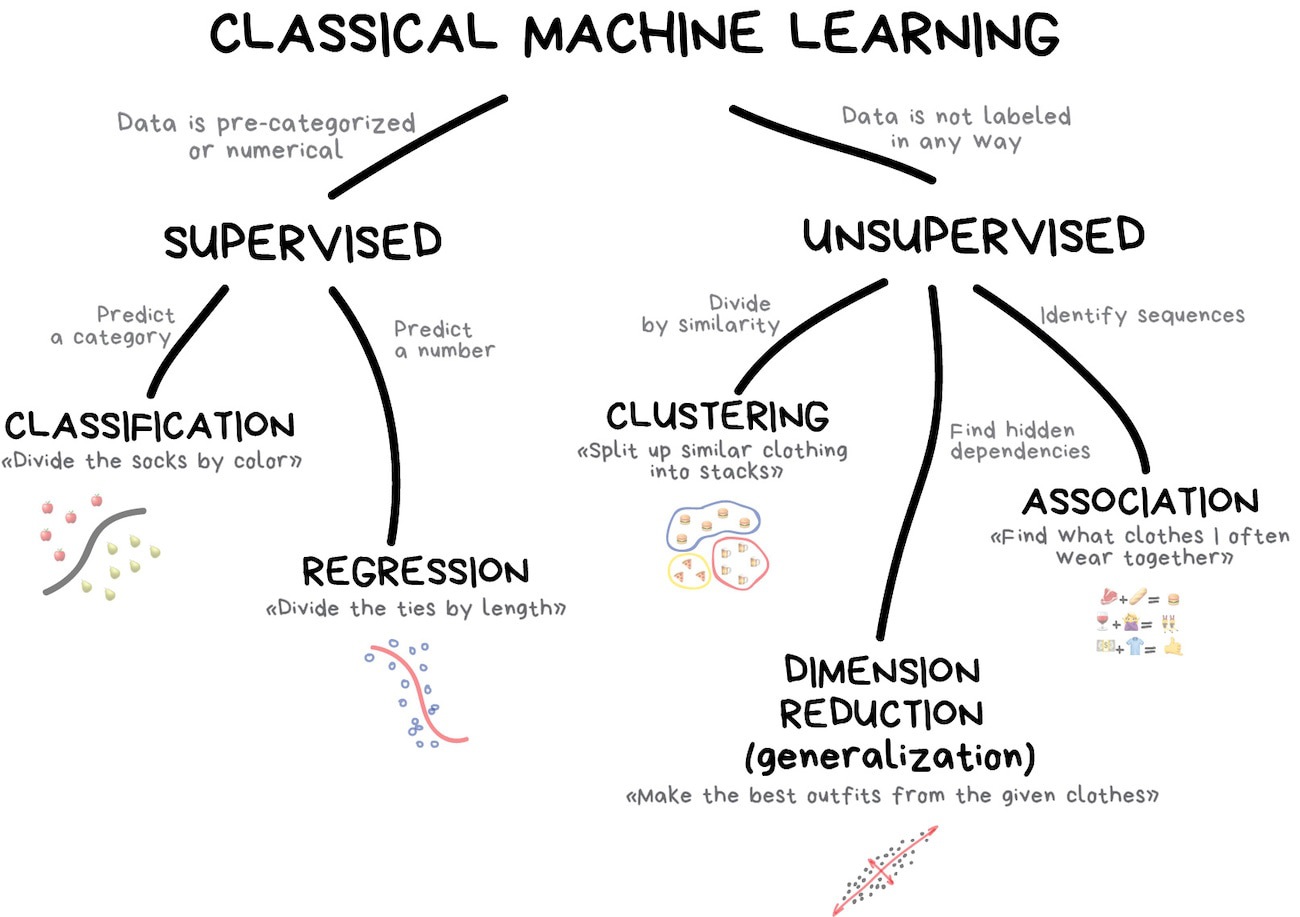
Dimension reduction

Transformation of data from a high-dimensional space into a low-dimensional space
Low-dimensional representation retains meaningful properties of the original data

Motivations for dimension reduction

Exploratory analysis and visualization
Resolving multicollinearity in regression features
Dealing with sparse data (curse of dimensionality)

Applications of dimension reduction

Measuring legislator ideology

What is political ideology? How do you measure it for a U.S. senator?

02:00

Defining ideology on a liberal-conservative spectrum

How do you locate legislators on this spectrum?
How liberal/conservative are members of the same political party?
How do you compare them over time (e.g. how liberal a Democrat was in 1870 vs. 1995)?

DW-NOMINATE

Use roll-call votes to measure ideology
- Over 100,000 recorded votes over time in the U.S. Congress
Dimension reduction to reduce the number of meaningful dimensions of variation across legislators over time
Results in two dimensions:
1. Political ideology
2. “Issue of the day” (e.g. slavery, civil rights, economic policy)

Polarization over time

Alternative measure: CFScores

Campaign Finance Scores (CFScores) measure the ideology of recipients and donors

Campaign contributions are public records in the United States
Assumes that donors give to candidates with similar ideologies/preferences
Unlike other techniques, allows for the standardized measurement of ideology of elected officials (legislators, executives, judges, etc.) and donors

Are they valid measures?

Polarization over time (CFScores)

Principal components analysis

Reduce the dimensionality of the data set through linear combinations of features \(X_1, X_2, \ldots, X_p\)
Common purposes
- Feature reduction
- Reduce multicollinearity
- Data visualization

Principal components

Explain most of the variability in the data with a smaller number of variables
Low-dimensional representation of high-dimensional data, with minimal information loss
Small number of dimensions
Linear combination of \(p\) features

Warning

Requires each of the original features to generate every component!

First principal component

Data set contains \(X_1, X_2, \ldots, X_p\) features
Create new set of \(Z_1, Z_2, \ldots, Z_p\) features

\[Z_1 = \phi_{11}X_1 + \phi_{21}X_2 + \dots + \phi_{p1}X_p\]

\(\max \mathrm{Var}(Z_1)\)
\(\phi_1\) - first principal component loading vector
- \(p\) individual loadings \(\phi_{11}, \dots, \phi_{p1}\)
Normalized \(\phi\)

\[\sum_{j=1}^p \phi_{j1}^2 = 1\]
- Requires normalized features

Second principal component

\[Z_2 = \phi_{12}X_1 + \phi_{22}X_2 + \dots + \phi_{p2}X_p\]

\[\max \mathrm{Var}(Z_2)\]

\(\sum_{j=1}^p \phi_{j2}^2 = 1\)
\(Z_1, Z_2\) uncorrelated (orthogonal)

\(n\)th principal component

\(\min(p, n)\) unique principal components
As \(j\) increases, variance of \(Z_j\) constantly decreasing

What does this give us?

Principal components are a new set of features
Each observation gets a score for each principal component
Each feature gets a loading on each principal component that identifies its contribution to and direction on that component

Fashion MNIST dataset

# A tibble: 60,000 × 785
   label  pixel1 pixel2 pixel3 pixel4 pixel5 pixel6 pixel7 pixel8 pixel9 pixel10
   <fct>   <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>   <dbl>
 1 Pullo…      0      0      0      0      0      0      0      0      0       0
 2 Ankle…      0      0      0      0      0      0      0      0      0       0
 3 Shirt       0      0      0      0      0      0      0      5      0       0
 4 T-shi…      0      0      0      1      2      0      0      0      0       0
 5 Dress       0      0      0      0      0      0      0      0      0       0
 6 Coat        0      0      0      5      4      5      5      3      5       6
 7 Coat        0      0      0      0      0      0      0      0      0       0
 8 Sandal      0      0      0      0      0      0      0      0      0       0
 9 Coat        0      0      0      0      0      0      3      2      0       0
10 Bag         0      0      0      0      0      0      0      0      0       0
# ℹ 59,990 more rows
# ℹ 774 more variables: pixel11 <dbl>, pixel12 <dbl>, pixel13 <dbl>,
#   pixel14 <dbl>, pixel15 <dbl>, pixel16 <dbl>, pixel17 <dbl>, pixel18 <dbl>,
#   pixel19 <dbl>, pixel20 <dbl>, pixel21 <dbl>, pixel22 <dbl>, pixel23 <dbl>,
#   pixel24 <dbl>, pixel25 <dbl>, pixel26 <dbl>, pixel27 <dbl>, pixel28 <dbl>,
#   pixel29 <dbl>, pixel30 <dbl>, pixel31 <dbl>, pixel32 <dbl>, pixel33 <dbl>,
#   pixel34 <dbl>, pixel35 <dbl>, pixel36 <dbl>, pixel37 <dbl>, …

PCA on pixel features

# A tibble: 3,000 × 5
   label           PC1     PC2   PC3     PC4
   <fct>         <dbl>   <dbl> <dbl>   <dbl>
 1 T-shirt/top  14.2    -9.75   1.12  3.01  
 2 Sneaker     -19.6    -2.02  -3.74 -4.04  
 3 Pullover     18.8     5.70  -6.47 -8.89  
 4 Bag          -1.63   -3.34   1.01 -1.00  
 5 Trouser       0.418 -16.9    7.09 -1.57  
 6 Dress         5.65  -15.9   11.7  -2.77  
 7 Shirt         2.93    0.149 -7.76  0.0737
 8 Sneaker     -19.2     0.278 -1.83 -7.83  
 9 Trouser      -0.161 -16.2    8.97 -1.46  
10 Dress         2.76   -7.08  -1.96  4.09  
# ℹ 2,990 more rows

PCA on pixel features

Compact visualization of principal components

Variance explained

Uniform Manifold Approximation and Projection (UMAP)

PCA assumes a linear combinations of features
UMAP uses a non-linear dimension reduction
Looks for a low-dimensional representation of the data that preserves the structure of the data as much as possible
Very useful for exploratory analysis (and potentially feature generation)

UMAP on fashion MNIST

Implementing dimension reduction with {recipes}

`step_pca()`

mnist_rec <- recipe(label ~ ., data = mnist_train) |>
  step_zv(all_numeric_predictors()) |>
  step_normalize(all_numeric_predictors()) |>
  step_pca(all_numeric_predictors())
mnist_rec

── Recipe ──────────────────────────────────────────────────────────────────────

── Inputs

Number of variables by role

outcome:     1
predictor: 784

── Operations

• Zero variance filter on: all_numeric_predictors()

• Centering and scaling for: all_numeric_predictors()

• PCA extraction with: all_numeric_predictors()

`prep()`

mnist_prep <- prep(mnist_rec)
mnist_prep

── Recipe ──────────────────────────────────────────────────────────────────────

── Inputs

Number of variables by role

outcome:     1
predictor: 784

── Training information

Training data contained 12000 data points and no incomplete rows.

── Operations

• Zero variance filter removed: <none> | Trained

• Centering and scaling for: pixel1, pixel2, pixel3, pixel4, ... | Trained

• PCA extraction with: pixel1, pixel2, pixel3, pixel4, pixel5, ... | Trained

`bake()`

bake(mnist_prep, new_data = NULL)

# A tibble: 12,000 × 6
   label          PC1    PC2    PC3    PC4    PC5
   <fct>        <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
 1 Ankle boot  -12.1   11.8   6.08   -2.92 -4.40 
 2 Shirt        20.5    1.82 -6.34   -3.37 -5.65 
 3 Dress        11.6  -11.6   7.60   -4.32 -0.642
 4 Bag         -13.8   -3.07 -9.50    6.63  0.513
 5 Sneaker     -17.9    6.91  3.19   -6.04 -0.128
 6 Coat         12.9   12.4  -9.23   -2.23 -1.06 
 7 T-shirt/top   3.80 -10.2   4.10    1.11  0.700
 8 Sneaker     -16.9    4.03 -0.902 -10.9   3.88 
 9 Trouser       7.13 -17.7  10.3    -3.62 -0.484
10 Sandal      -17.2    2.05 -2.94   14.4  -0.434
# ℹ 11,990 more rows

`tidy()`

tidy(mnist_prep, 3)

# A tibble: 614,656 × 4
   terms     value component id       
   <chr>     <dbl> <chr>     <chr>    
 1 pixel1  0.00144 PC1       pca_yA0w4
 2 pixel2  0.00121 PC1       pca_yA0w4
 3 pixel3  0.00270 PC1       pca_yA0w4
 4 pixel4  0.00286 PC1       pca_yA0w4
 5 pixel5  0.00303 PC1       pca_yA0w4
 6 pixel6  0.00457 PC1       pca_yA0w4
 7 pixel7  0.00565 PC1       pca_yA0w4
 8 pixel8  0.00877 PC1       pca_yA0w4
 9 pixel9  0.0135  PC1       pca_yA0w4
10 pixel10 0.0184  PC1       pca_yA0w4
# ℹ 614,646 more rows

`tidy()`

tidy(mnist_prep, 3, type = "variance") |>
  count(terms)

# A tibble: 4 × 2
  terms                           n
  <chr>                       <int>
1 cumulative percent variance   784
2 cumulative variance           784
3 percent variance              784
4 variance                      784

Information from `prep()`

Stuff about the features - tidy()
Stuff about the observations - bake()

Application exercise

`ae-10`

Go to the course GitHub org and find your ae-10 (repo name will be suffixed with your GitHub name).
Clone the repo in RStudio, run renv::restore() to install the required packages, open the Quarto document in the repo, and follow along and complete the exercises.
Render, commit, and push your edits by the AE deadline – end of the day

Wrap-up

Recap

Unsupervised learning is about finding patterns/structure in data
Dimension reduction reduce a data set from a high-dimensional space to a low-dimensional space
Dimension reduction is useful for visualization, noise reduction, and feature generation
PCA is a linear dimension reduction technique that finds the directions of maximum variance in the data

Dimension reduction

Announcements

Announcements

Learning objectives

What is unsupervised learning?

Dimension reduction